
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
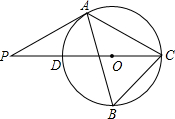 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,PA是⊙O的切线;
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,PA是⊙O的切线;| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
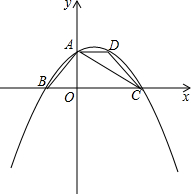 如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2
如图,在平面直角坐标系中,四边形ABCD是等腰梯形,AD∥BC,AB=DC,BC在x轴上,点A在y轴的正半轴上,点A,D的坐标分别为A(0,2),D(2,2),AB=2| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 时,每个元件的状态有两种可能:通过或断开,并且这两种状态的可能性相等.
时,每个元件的状态有两种可能:通过或断开,并且这两种状态的可能性相等.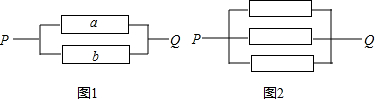
查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
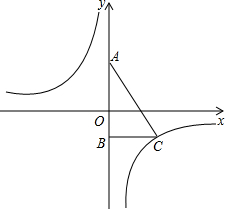 如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,-2),BC的长为3,反比例函数y=
如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,-2),BC的长为3,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
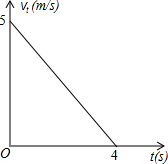 一个小球以初始速度v0=5m/s运动,并且均匀减速,4s后停止运动,下图是运动时间t(s)与第t秒末的速度vt(m/s)的函数图象,下表是小球t秒内所走的路与时间的一些数据:
一个小球以初始速度v0=5m/s运动,并且均匀减速,4s后停止运动,下图是运动时间t(s)与第t秒末的速度vt(m/s)的函数图象,下表是小球t秒内所走的路与时间的一些数据:| 时间t(s) | 0 | 1 | 2 | 3 | 4 |
| 路程(m) | 0 | 4.375 | 7.5 | 9.375 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com