
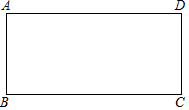
 如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°.
如图,在四边形ABCD中,已知AB∥DC,AB=DC,在不添加任何辅助线的情况下,请补充一个条件,使四边形ABCD成为矩形,这个条件是∠A=90°. 科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{\frac{x}{15}-15=y}\\{\frac{x}{12}+12=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\frac{x}{15}+15=y}\\{\frac{x}{12}-12=y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{x}{15}-\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{15}+\frac{24}{60}=y}\\{\frac{x}{12}-\frac{15}{60}=y}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
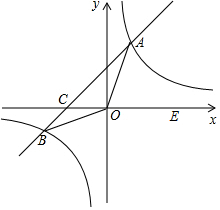 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{12}{x}$的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(-6,n);E为x轴正半轴上一点,且tan∠AOE=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)
仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是2≤x≤5.
如图,在矩形纸片ABCD中,AB=5,AD=2,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原,则四边形EPFD为菱形时,x的取值范围是2≤x≤5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com