
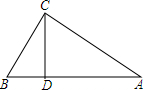
 如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1:$\sqrt{3}$的一对相似三角形;(不妨如图假设左小右大),求:
如图,D为△ABC边AB上一点,且CD分△ABC为两个相似比为1:$\sqrt{3}$的一对相似三角形;(不妨如图假设左小右大),求:分析 (1)根据相似三角形面积的比等于相似比的平方解答;
(2)根据锐角三角函数的概念解答即可.
解答 解:(1)∵△BCD和△CAD的相似比为1:$\sqrt{3}$,
∴△BCD和△CAD的面积比为1:3;
(2)∵△BCD∽△CAD,
∴∠BDC=∠ADC=90°,
tanA=$\frac{CD}{AD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
tanB=$\frac{CD}{BD}$=$\sqrt{3}$,
∴∠B=60°,
∴∠ACB=90°.
点评 本题考查的是相似三角形的性质,掌握相似三角形面积的比等于相似比的平方以及锐角三角函数的概念是解题的关键.


科目:初中数学 来源: 题型:解答题
 李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案:
李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
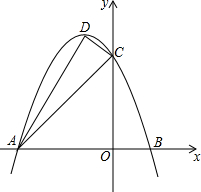 如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.
如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5 | B. | 2 | C. | 1 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是__cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com