Question

已知a，b，c，d均为实数，且ad-bc=1，a²+b²+c²+d²-ab+cd=1，则abcd=________．

Answer 1

分析：根据已知条件写成等式2a²+2b²+2c²+2d²-2ab+2cd=2ad-2bc，进一步写成完全平方的形式（a-b）²+（c+d）²+（a-d）²+（b+c）²=0，据此求解．
解答：∵a²+b²+c²+d²-ab+cd=1，
且ad-bc=1（1），
∴a²+b²+c²+d²-ab+cd=ad-bc，
∴2a²+2b²+2c²+2d²-2ab+2cd=2ad-2bc，
∴（a-b）²+（c+d）²+（a-d）²+（b+c）²=0，
∴a-b=c+d=a-d=b+c=0，
∴a=b=d=-c（2），
把（2）代入（1）得：a²+a²=1，
∴，
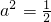
∴abcd=a•a•（-a）•a=-=-．
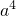
故答案为：-．
点评：此题主要考查完全平方公式，多个非负数相加为0，则都等于0．
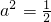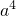