
 如图,在正方形网格中,每个小正方形的边长都是个1单位长度,△ABC的三个顶点都在格点上.
如图,在正方形网格中,每个小正方形的边长都是个1单位长度,△ABC的三个顶点都在格点上.分析 (1)根据平移的方向和距离进行作图即可;
(2)根据关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分进行作图;
(3)过轴对称来确定,即作出其中一点关于直线MN的对称点,对称点与另一点的连线与直线MN的交点就是所要找的点.
解答 解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)如图所示,作点B关于MN的对称点B',连接AB',交MN于一点,则该点即为点P.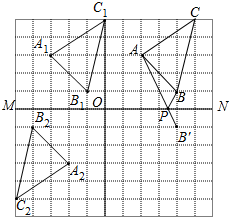
点评 本题主要考查了利用图形的基本变换进行作图,解题时注意,凡是涉及最短距离的问题,一般要考虑线段的性质定理,根据轴对称变换来解决,多数情况要作点关于某直线的对称点.


科目:初中数学 来源: 题型:选择题
| A. | (-5,2) | B. | (-5,6) | C. | (-5,-6) | D. | (-5,6)或(-5,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com