
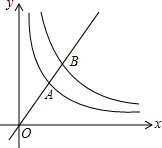
 如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$.
如图,在平面直角坐标系中,O为原点,直线y=kx(k>0)与双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)分别交于A,B两点,则$\frac{OB}{OA}$=$\sqrt{2}$. 分析 根据直线y=kx(k>0)先设出A、B两点的坐标,作辅助线构建两个直角三角形,利用平行相似得比例式得出$\frac{OB}{OA}$等于A、B两点的纵坐标之比,由双曲线y=$\frac{3}{x}(x>0),y=\frac{6}{x}$(x>0)计算出结论.
解答  解:设A(a,ka)、B(b,kb),
解:设A(a,ka)、B(b,kb),
分别过点A、B向x轴作垂线,垂足分别为C、D,
则AC∥BD,
∴△AOC∽△BOD,
∴$\frac{OB}{OA}$=$\frac{BD}{AC}$=$\frac{kb}{ka}$=$\frac{b}{a}$,
∵点A在双曲线y=$\frac{3}{x}$上,
∴ka2=3,k=$\frac{3}{{a}^{2}}$,
∵点B在双曲线y=$\frac{6}{x}$上,
∴kb2=6,k=$\frac{6}{{b}^{2}}$,
∴$\frac{3}{{a}^{2}}=\frac{6}{{b}^{2}}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=2,
∵A、B在第一象限,则a>0,b>0,
∴$\frac{b}{a}$=$\sqrt{2}$,
∴$\frac{OB}{OA}$=$\frac{b}{a}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了反比例函数与一次函数的交点,解此类题的思路为:先根据一个函数表示出交点的坐标,再利用另一个函数列方程或比例式求解,综合性较强.此题还通过作坐标轴的垂线构建相似三角形或全等三角形,利用它们的性质列式计算.


科目:初中数学 来源: 题型:选择题
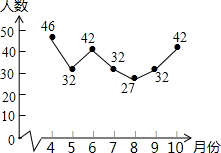 在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )| A. | 46人 | B. | 42人 | C. | 32人 | D. | 27人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
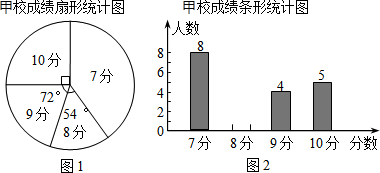 甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表| 分数 | 7分 | 8分 | 9分 | 10分 |
| 人数 | 11 | 0 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
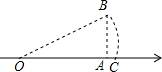 如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )
如图,数轴上点A对应的数为2,AB⊥OA于A,且AB=1,以原点O为圆心,OB为半径画弧,交数轴于点C,则OC的长为( )| A. | 2 | B. | 3 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com