
 已知一次函数y=kx+3(k<0)的图象与x轴、y轴分别相交于点A、B,tan∠OAB=2,点P(a,b)是在该函数的图象上的一点.
已知一次函数y=kx+3(k<0)的图象与x轴、y轴分别相交于点A、B,tan∠OAB=2,点P(a,b)是在该函数的图象上的一点.分析 (1)首先求得B的坐标,然后根据三角函数的定义求得OA的长,即可求得A的坐标,然后利用待定系数法求得一次函数;
(2)把P(a,b)代入y=-2x+3,然后根据题意得出|a|=2-|b|,解得即可.
(3)求出P的坐标,分为两种情况m>0,m<0,根据坐标即可得出不等式组,求出不等式组的解集即可.
解答 解:(1)在y=kx+3中令x=0,则y=3,即B的坐标是(0,3),OB=3.
∵tan∠BAO=$\frac{OB}{OA}$=2,
∴OA=$\frac{3}{2}$.
∴A的坐标是($\frac{3}{2}$,0).
代入y=kx+3得0=$\frac{3}{2}$k+3,解得k=-2,
∴一次函数的解析式是y=-2x+3.
(2)∵点P(a,b)是在该函数的图象上的一点,
∴b=-2a+3,
∵点P到x轴、y轴的距离之和等于2,
∴|a|=2-|b|,
∴|a|=2-|-2a+3|,
当a<0时,则有-a=2+2a-3,
解得a=$\frac{1}{3}$(不合题意舍去),
当0<a<$\frac{3}{2}$时,则有a=2+2a-3,
解得a=1,
∴P(1,1),
当a>$\frac{3}{2}$时,则有a=2-2a+3,
解得a=$\frac{5}{3}$,
∴P($\frac{5}{3}$,-$\frac{1}{3}$);
(3)由已知P(1-m,2m+1),易知,a≠b,1-m≠2m+1,m≠0;
若m>0,a<1<b,由题设a≥0,b≤2,
则 1-m<1,2m+1≤2,
解不等式组的解集是:0<m≤$\frac{1}{2}$;
若m<0,b<1<a,由题设b≥0,a≤2,
则 1-m>1,2m+1≥0,
解得:-$\frac{1}{2}$≤m<0;
综合上述:m的取值范围是:$-\frac{1}{2}≤m≤\frac{1}{2}且m≠0$.
点评 本题考查了待定系数法求一次函数解析式,以及三角函数的定义,解答本题的涉及多方面知识,难度一般.


科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{5}$ | B. | ±$\sqrt{5}$ | C. | $\sqrt{-5}$ | D. | $\sqrt{(-5)^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
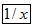 ,能求出输入的不为零的数的倒数(注:有时需先按
,能求出输入的不为零的数的倒数(注:有时需先按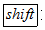 或
或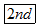 键,才能实现此功能,下面不再说明).例如,输入2,按下键
键,才能实现此功能,下面不再说明).例如,输入2,按下键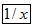 ,则得0.5.现在计算器上输入某数,再依下列顺序按键:
,则得0.5.现在计算器上输入某数,再依下列顺序按键: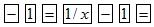 ,在显示屏上的结果是-0.75,则原来输入的某数是5.
,在显示屏上的结果是-0.75,则原来输入的某数是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-3,n),B(2,-3)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com