练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如果$\frac{a}{15}$是真分数，$\frac{a}{12}$是假分数，那么满足条件的正整数a有（　　）
    A．1个B．2个C．3个D．4个

    分析 根据真分数与假分数的意义可知，真分数的分子＜分母，真分数＜1，假分数的分子≥分母，假分数≥1，所以12≤a＜15．即a可为12，13，14．满足条件的正整数a有3个．

    解答 解：因为真分数＜1，假分数＞1，
    所以，12≤a＜15，
    即a可为12，13，14．满足条件的正整数a有3个．
    故选：C．

    点评 本题主要考查了有理数的众数，此题主要根据真分数与假分数的意义进行解答即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．如图，长为a，宽为b的长方形的周长为14，面积为10，则a2+b2的值为（　　）
    A．140B．70C．35D．29

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．按数字排列规律：$\frac{1}{2}$，-$\frac{2}{5}$，$\frac{3}{10}$，-$\frac{4}{17}$，…，写出第10个数为-$\frac{10}{101}$（n为正整数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．单项式-32x2y3的系数和次数分别是（　　）
    A．-3，5B．9，7C．-9，7D．-9，5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在△ABC中，AB=AC，以AB为直径的半圆O分别交AC、BC于点D、E．
    （1）求证：点E是BC的中点．
    （2）若∠BOD=80°，求∠CED的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，（单位：厘米），求半圆柱木料的表面积和体积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

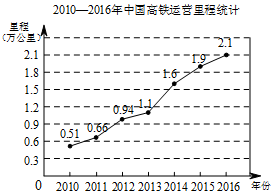    13．2016年我国高铁运营里程突破2万公里，占世界总里程的60%以上．如图，是我国2010-2016年高铁运营里程情况统计，根据统计图提供的信息，预估2017年我国高铁运营里程约为2.3万公里，你的预估理由是2016到2017年的增幅与2015到2016的增幅最相近．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列说法正确的是（　　）
    A．若a+b=0，则$\frac{a}{b}$=-1B．若|a|=-a，则a＜0
    C．若a＞b＞0，则-a＜-b＜0D．若a＜b＜0，则$\frac{1}{a}$＜$\frac{1}{b}$＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如果抛物线C1的顶点在抛物线C2上，同时，抛物线C2的顶点在抛物线C1上，那么，我们称抛物线C1与C2关联．
    （1）已知抛物线y=x2+2x-1，判断下列抛物线：①y=-x2+2x+1；②y=-2x2+4x+4与已知抛物线是否关联，并说明理由；
    （2）已知抛物线C1：y=$\frac{1}{2}$x2-x-$\frac{3}{2}$，点P的坐标为（t，-1），将抛物线绕点P旋转180°得到抛物线C2（此处我们称点P为旋转点），若抛物线C1与C2关联，求抛物线C2的解析式；
    （3）在（2）的条件下，已知点A（4，y0）是抛物线C1上的一点，求以点A为顶点并与抛物线C1相关联的抛物线C3的解析式，并判断此时抛物线C3能否由抛物线C1旋转得来？若能，请求出旋转点坐标；若不能，请说明你的理由；
    （4）由上述结论猜想：若两抛物线C1、C2相关联，则它们的二次式项系数（分别记为a1，a2）应满足数量关系：a1+a2=0．
    参考公式（中点坐标公式）：若点A（x1，y1），B（x2，y2），则线段AB的中点坐标为（$\frac{{x}_{1}+{x}_{2}}{2}$，$\frac{{y}_{1}+{y}_{2}}{2}$）．

    查看答案和解析>>

    同步练习册答案