
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球.求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为![]() .求n的值.
.求n的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)4.
;(3)4.
【解析】试题分析: (1)由一个不透明的布袋里装有3个球,其中2个红球,1个白球,根据概率公式直接求解即可求得答案;
(2)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率;
(3)根据概率公式列方程,解方程即可求得n的值.
解:(1)∵一个不透明的布袋里装有3个球,其中2个红球,1个白球,
∴摸出1个球是白球的概率为![]() ;
;
(2)画树状图、列表得:
| 白 | 红1 | 红2 |
白 | 白,白 | 白,红1 | 白,红2 |
红1 | 红1,白 | 红1,红1 | 红1,红2 |
红2 | 红2,白 | 红2,红1 | 红2,红2 |
∴一共有9种等可能的结果,两次摸出的球恰好颜色不同的有4种,
∴两次摸出的球恰好颜色不同的概率为![]() ;
;
(3)由题意得: ![]() ,
,
解得:n=4.
经检验,n=4是所列方程的解,且符合题意,
∴n=4.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),把△ABC平移之后得到△A′B′C′,并且C的对应点C′的坐标为(4,1).
(1)分别写出A′、B′两点的坐标;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知AB=AC,D为∠BAC的角平分线上面一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上面两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上面三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第n个图形中有全等三角形的对数是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.每天销售量(y件)与销售单价x(元/件)的函数关系式是y=﹣10x+700
(1)当销售单价定为多少时,试销该工艺品每天获得的利润最大?最大利润是多少?
(2)市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行研学旅行活动,车上准备了7箱矿泉水,每箱的瓶数相同,到达目的地后,先从车上搬下3箱,发给每位同学1瓶矿泉水,有9位同学未领到.接着又从车上搬下4箱,继续分发,最后每位同学都有2瓶矿泉水,还剩下6瓶.问:有多少人参加此次研学旅行活动?每箱矿泉水有多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABDC中,AB=6,E在CD上,DE=2,将△ADE沿AE折叠至△AFE,延长EF交BC于G,连AG、CF,下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④![]() FCG=3,其中正确的有( ).
FCG=3,其中正确的有( ).
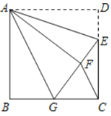
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=8,将纸片沿EF折叠,使点C与点A重合,则下列结论错误的是( )

A. AF=AE B. △ABE≌△AGF C. EF=![]() D. AF=EF
D. AF=EF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com