
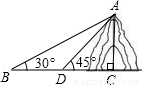
 如图所示,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,则山高为
如图所示,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,则山高为 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:三点一测丛书 八年级数学 下 (北京师大版课标本) 北京师大版课标本 题型:044
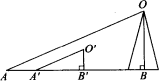
古代一位数学家想出了一种测量某山高的方法:如图所示,为了测量山的高度OB,先竖一根已知长度的木棒![]() ,比较棒子的影长
,比较棒子的影长![]() 与山的影长AB,即可近似算出山的高度OB.如果
与山的影长AB,即可近似算出山的高度OB.如果![]() =1 m,
=1 m,![]() =2 m,AB=274 m,求山的高度OB.
=2 m,AB=274 m,求山的高度OB.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
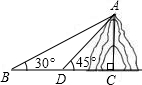 如图所示,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,则山高为________.
如图所示,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,则山高为________.查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:《28.2 解直角三角形》2009年同步练习(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com