
分析 利用抛物线的对称性得到抛物线与x轴的交点坐标为(1,0),(5,0),利用二次函数的最大值问题得到抛物线的顶点坐标为(3,10),则可设交点式y=a(x-1)(x-5),然后把顶点坐标代入求出a即可.
解答 解:∵当x=3时,抛物线在x轴上截得的线段长为4,
∴抛物线与x轴的交点坐标为(1,0),(5,0),
∵当x=3时,函数取最大值10,
∴抛物线的顶点坐标为(3,10),
设抛物线的解析式为y=a(x-1)(x-5),
把(3,10)代入得a•2•(-2)=10,解得a=-$\frac{5}{2}$,
∴抛物线的解析式为y=-$\frac{5}{2}$(x-1)(x-5),
即y=-$\frac{5}{2}$x2+15x-$\frac{25}{2}$.
点评 本题考查了抛物线与x轴的交点:利用抛物线与x轴的交点坐标(x1,0),(x2,0)可设二次函数的解析式为:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
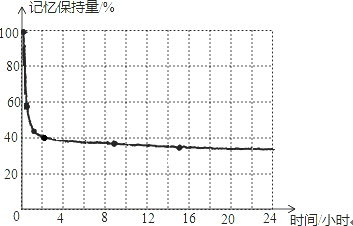 德国心理学家艾宾浩斯(H•Ebbinghaus)研究发现,遗忘在学习之后立即开始,遗忘是有规律的.他用无意义音节作记忆材料,用节省法计算保持和遗忘的数量.通过测试,他得到了一些数据,根据这些数据绘制出一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如图.该曲线对人类记忆认知研究产生了重大影响.小梅观察曲线,得出以下四个结论:
德国心理学家艾宾浩斯(H•Ebbinghaus)研究发现,遗忘在学习之后立即开始,遗忘是有规律的.他用无意义音节作记忆材料,用节省法计算保持和遗忘的数量.通过测试,他得到了一些数据,根据这些数据绘制出一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如图.该曲线对人类记忆认知研究产生了重大影响.小梅观察曲线,得出以下四个结论:| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购苹果数 | 不超过30kg | 30kg以下但不超过50kg | 50kg以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
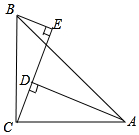 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com