练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

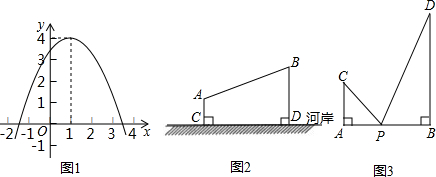
    二次函数的最大(小)值的求法主要有两种：(1)直接代入抛物线顶点纵坐标的公式计算；(2)把函数关系式配方成y＝a(x＋h)2＋k的形式，利用非负数的性质可得，当a＞0时，最小值就是________；当a＜0时，最大值就是________．

    答案：k,k
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2011•新华区一模）我们知道：根据二次函数的图象，可以直接确定二次函数的最大（小）值；根据“两点之间，线段最短”，并运用轴对称的性质，可以在一条直线上找到一点，使得此点到这条直线同侧两定点之间的距离之和最短．
    这种数形结合的思想方法，非常有利于解决一些数学和实际问题中的最大（小）值问题．请你尝试解决一下问题：
    （1）在图1中，抛物线所对应的二次函数的最大值是
    4
    4
    ；
    （2）在图2中，相距3km的A、B两镇位于河岸（近似看做直线l）的同侧，且到河岸的距离AC=1千米，BD=2千米，现要在岸边建一座水塔，分别直接给两镇送水，为使所用水管的长度最短，请你：
    ①作图确定水塔的位置；
    ②求出所需水管的长度（结果用准确值表示）
    （3）已知x+y=6，求
    		x2+9
    +
    		y2+25
    的最小值；
    此问题可以通过数形结合的方法加以解决，具体步骤如下：
    ①如图3中，作线段AB=6，分别过点A、B，作CA⊥AB，DB⊥AB，使得CA=
    3
    3
    ，DB=
    5
    5
    ；
    ②在AB上取一点P，可设AP=
    x
    x
    ，BP=
    y
    y
    ；
    ③
    		x2+9
    +
    		y2+25
    的最小值即为线段
    PC
    PC
    和线段
    PD
    PD
    长度之和的最小值，最小值为
    10
    10
    ．

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（四川达州卷）数学（带解析） 题型：解答题

    问题背景
    若矩形的周长为1，则可求出该矩形面积的最大值.我们可以设矩形的一边长为x，面积为s，则s与x的函数关系式为： ，利用函数的图象或通过配方均可求得该函数的最大值.
    提出新问题
    若矩形的面积为1，则该矩形的周长有无最大值或最小值？若有，最大（小）值是多少？
    分析问题
    若设该矩形的一边长为x，周长为y，则y与x的函数关系式为：，问题就转化为研究该函数的最大（小）值了.
    解决问题
    借鉴我们已有的研究函数的经验，探索函数的最大（小）值.
    （1）实践操作：填写下表，并用描点法画出函数的图象：

    x
    		···



    		1
    		2
    		3
    		4
    		···
    y
    		 
    		 
    		 
    		 
    		 
    		 
    		 
    		 
    		 
     

    （2）观察猜想：观察该函数的图象，猜想当x=        时，函数有最   值（填
    “大”或“小”），是         .
    （3）推理论证：问题背景中提到，通过配方可求二次函数的最大值，请你尝试通过配方求函数的最大（小）值，以证明你的猜想. 〔提示：当时，〕

    查看答案和解析>>

    科目：初中数学 来源：2013届北京市西城区（北区）九年级上学期期末考试数学试卷（带解析） 题型：解答题

    阅读下面的材料：
    小明在学习中遇到这样一个问题：若1≤x≤m，求二次函数的最大值．他画图研究后发现，和时的函数值相等，于是他认为需要对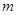进行分类讨论．
    他的解答过程如下：
    ∵二次函数的对称轴为直线，
    ∴由对称性可知，和时的函数值相等．
    ∴若1≤m＜5，则时，的最大值为2；
    若m≥5，则时，的最大值为．

    请你参考小明的思路，解答下列问题：
    （1）当≤x≤4时，二次函数的最大值为_______；
    （2）若p≤x≤2，求二次函数的最大值；
    （3）若t≤x≤t+2时，二次函数的最大值为31，则的值为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    我们知道：根据二次函数的图象，可以直接确定二次函数的最大（小）值；根据“两点之间，线段最短”，并运用轴对称的性质，可以在一条直线上找到一点，使得此点到这条直线同侧两定点之间的距离之和最短．
    这种数形结合的思想方法，非常有利于解决一些数学和实际问题中的最大（小）值问题．请你尝试解决一下问题：
    （1）在图1中，抛物线所对应的二次函数的最大值是______；
    （2）在图2中，相距3km的A、B两镇位于河岸（近似看做直线l）的同侧，且到河岸的距离AC=1千米，BD=2千米，现要在岸边建一座水塔，分别直接给两镇送水，为使所用水管的长度最短，请你：
    ①作图确定水塔的位置；
    ②求出所需水管的长度（结果用准确值表示）
    （3）已知x+y=6，求数学公式+数学公式的最小值；
    此问题可以通过数形结合的方法加以解决，具体步骤如下：
    ①如图3中，作线段AB=6，分别过点A、B，作CA⊥AB，DB⊥AB，使得CA=______，DB=______；
    ②在AB上取一点P，可设AP=______，BP=______；
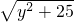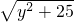    ③数学公式+数学公式的最小值即为线段______和线段______长度之和的最小值，最小值为______．

    查看答案和解析>>

    科目：初中数学 来源：2011年河北省石家庄市新华区中考数学一模试卷（解析版） 题型：解答题

    我们知道：根据二次函数的图象，可以直接确定二次函数的最大（小）值；根据“两点之间，线段最短”，并运用轴对称的性质，可以在一条直线上找到一点，使得此点到这条直线同侧两定点之间的距离之和最短．
    这种数形结合的思想方法，非常有利于解决一些数学和实际问题中的最大（小）值问题．请你尝试解决一下问题：
    （1）在图1中，抛物线所对应的二次函数的最大值是______；
    （2）在图2中，相距3km的A、B两镇位于河岸（近似看做直线l）的同侧，且到河岸的距离AC=1千米，BD=2千米，现要在岸边建一座水塔，分别直接给两镇送水，为使所用水管的长度最短，请你：
    ①作图确定水塔的位置；
    ②求出所需水管的长度（结果用准确值表示）
    （3）已知x+y=6，求+的最小值；
    此问题可以通过数形结合的方法加以解决，具体步骤如下：
    ①如图3中，作线段AB=6，分别过点A、B，作CA⊥AB，DB⊥AB，使得CA=______，DB=______；
    ②在AB上取一点P，可设AP=______，BP=______；
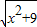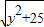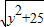    ③+的最小值即为线段______和线段______长度之和的最小值，最小值为______．

    查看答案和解析>>

    同步练习册答案