
【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.


(1)试判断△ABC的形状,并说明理由;
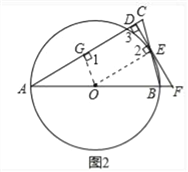
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=![]() ,求⊙O的半径和BF的长
,求⊙O的半径和BF的长
【答案】(1)△ABC是等腰三角形,理由见解析;
(2)⊙O的半径为2,BF=![]() ﹣2 .
﹣2 .
【解析】分析:(1)连接OE,根据切线性质得OE⊥DE,与已知中的ED⊥AC得平行,由此得∠1=∠C,再根据同圆的半径相等得∠1=∠B,可得出三角形为等腰三角形;
(2)通过作辅助线构建矩形OGDE,再设与半径有关系的边OG=x,通过AB=AC列等量关系式,可求得结论.
本题解析:
解:(1)△ABC是等腰三角形,理由是:
如图1,连接OE,
∵DE是⊙O的切线,
∴OE⊥DE,∵ED⊥AC,∴AC∥OE,∴∠1=∠C,∵OB=OE,∴∠1=∠B,
∴∠B=∠C,∴△ABC是等腰三角形;
(2)如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°﹣75°﹣75°=30°,
设OG=x,则OA=OB=OE=2x,AG=x,
∴DG=0E=2x,
根据AC=AB得:4x=![]() x+2x+2-
x+2x+2-![]() , x=1,∴0E=OB=2,
, x=1,∴0E=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
cos30=![]() ,OF=
,OF=![]() =
=![]() ,
,
∴BF=![]() ﹣2,⊙O的半径为2.
﹣2,⊙O的半径为2.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB:y=一 ![]() x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,
x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0, ![]() ),与直线AB交于点E.
),与直线AB交于点E.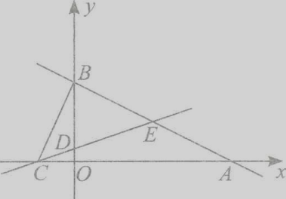
(1)求直线CD的函数关系式;
(2)连接BC,求△BCE的面积;
(3)设点Q的坐标为(m,2),求m的值使得QA+QE值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
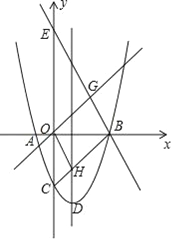
【题目】如图,抛物线y=x2﹣(m+2)x+3(m﹣1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=﹣2x+m+6经过点B,交y轴于点E(0,6).
(1)求直线和抛物线的解析式;
(2)如果抛物线的对称轴与线段BC交于点H,且直线y=x与直线y=﹣2x+m+6交于点G,求证:四边形OHBG是平行四边形;
(3)在抛物线上是否存在点P,使△APB的面积等于平行四边形OHBG的面积,若存在,直接写出P点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△DCB,若BC=10cm,AB=6cm,AC=7cm,则CD为( )
A. 10cm B. 7cm C. 6cm D. 6cm或7cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初步测算,2015年海宁市全年实现地区生产总值700.23亿元,比上年增长6.7%.其中700.23亿用科学记数法表示为( )
A.700.23×108
B.70.023×109
C.7.0023×1010
D.7.0023×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心,他们捐款的数额分别是(单位:元)50、20、50、30、25、50、55,这组数据的众数和中位数分别是( )
A.50元,30元
B.50元,40元
C.50元,50元
D.55元,50元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com