
| a2+1 |
| b2+4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 解:∵a,b均为正数,a+b=2,b=2-a,
解:∵a,b均为正数,a+b=2,b=2-a,| a2+1 |
| b2+4 |
| a2+1 |
| (2-a)2+22 |
| 13 |
| 13 |


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
| 5 |
| 10 |
| 13 |
| 5 |
| 2 |
| 17 |
| m2+16n2 |
| 9m2+4n2 |
| m2+n2 |
| a2+4 |
| b2+25 |
| a2-d2 |

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 ≤1
≤1 ≤
≤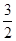
 ≤ 3
≤ 3 ≤ ;
≤ ;查看答案和解析>>
科目:初中数学 来源:2011届江苏南京市第三初级中学九年级上学期期中考试数学卷(带解析) 题型:解答题
阅读下面的材料,并解答问题:
材料:已知当a、b是正数时,有下列命题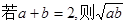 ≤1
≤1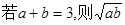 ≤
≤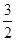
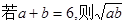 ≤ 3
≤ 3
(1)根据以上三个命题所提供的规律猜想: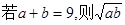 ≤ ;
≤ ;
(2)以上规律可用字母表示为 ;
(3)建造一个容积为8立方米,深2米的长方形无盖水池,池底和池壁的造价分别为每平方米120元和80元. 设池底的长为x米,水池总造价为y元,应用上述的规律,求水池的最低造价.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏南京市九年级上学期期中考试数学卷(解析版) 题型:解答题
阅读下面的材料,并解答问题:
材料:已知当a、b是正数时,有下列命题
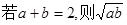 ≤1
≤1
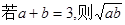 ≤
≤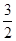
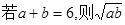 ≤ 3
≤ 3
(1)根据以上三个命题所提供的规律猜想: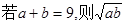 ≤
;
≤
;
(2)以上规律可用字母表示为 ;
(3)建造一个容积为8立方米,深2米的长方形无盖水池,池底和池壁的造价分别为每平方米120元和80元. 设池底的长为x米,水池总造价为y元,应用上述的规律,求水池的最低造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com