
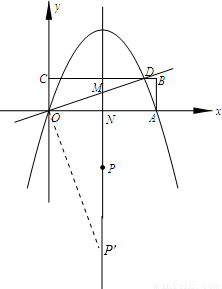
矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(10,0)、C(0,3),直线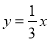 与BC相交于点D,抛物线y=ax2+bx经过A、D两点.
与BC相交于点D,抛物线y=ax2+bx经过A、D两点.

(1)求抛物线的解析式;
(2)连接AD,试判断△OAD的形状,并说明理由.
(3)若点P是抛物线的对称轴上的一个动点,对称轴与OD、x轴分别交于点M、N,问:是否存在点P,使得以点P、O、M为顶点的三角形与△OAD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)y=- x2+
x2+ x.;(2)△OAD是直角三角形.(3)(5,0)或(5,-15)
x.;(2)△OAD是直角三角形.(3)(5,0)或(5,-15)
【解析】
试题分析:(1)根据题意可得出点D的纵坐标为3,代入直线解析式可得出点D的横坐标,从而将点D和点A的坐标代入可得出抛物线的解析式.
(2)分别求出OA、OD、AD的长度,继而根据勾股定理的逆定理可判断出△OAD是直角三角形.
(3)①由图形可得当点P和点N重合时能满足△OPM∽△ODA,②过点O作OD的垂线交对称轴于点P′,此时也可满足△P′OM∽△ODA,利用相似的性质分别得出点P的坐标即可.
试题解析:(1)由题意得,点D的纵坐标为3,
∵点D在直线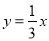 上,
上,
∴点D的坐标为(9,3),
将点D(9,3)、点A(10,0)代入抛物线可得:
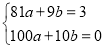 ,
,
解得: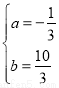
故抛物线的解析式为:y=- x2+
x2+ x.
x.
(2)∵点D坐标为(9,3),点A坐标为(10,0),
∴OA=10,OD=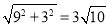 ,AD=
,AD=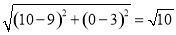 ,
,
从而可得OA2=OD2+AD2,
故可判断△OAD是直角三角形.
(3)①由图形可得当点P和点N重合时能满足△OPM∽△ODA,
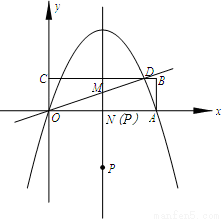
此时∠POM=∠DOA,∠OPM=∠ODA,
故可得△OPM∽△ODA,OP=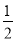 OA=5,
OA=5,
即可得此时点P的坐标为(5,0)
②过点O作OD的垂线交对称轴于点P′,此时也可满足△P′OM∽△ODA,
由题意可得,点M的横坐标为5,代入直线方程可得点M的纵坐标为 ,
,
故可求得OM=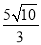
∵∠OP′M+∠OMN=∠DOA+∠OMN=90°,
∴∠OP′M=∠DOA,
∴△P′OM∽△ODA,
故可得 ,
,
即
解得:MP′=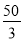 ,
,
又∵点M的纵坐标= ,
,
∴P′N=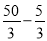 =15,
=15,
即可得此时点P′的坐标为(5,-15)
综上可得存在这样的点P,点P的坐标为(5,0)或(5,-15)
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年江苏省靖江市八年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,直线y1=x+b与y2=kx﹣1相交于点P,点P的横坐标为﹣1,则关于x的不等式x+b>kx﹣1的解集 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,DE是△ABC中边AC的垂直平分线,若BC=18 cm, AB=10 cm,则△ABD的周长为

A.16 cm B.18 cm C.26 cm D.28 cm
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省宁津县九年级上学期期末质量检测数学试卷(解析版) 题型:解答题
解方程.(1)(3x-4)2=(4x-3)2
(2)(2y+1)2+3(2y+1)+2=0.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省宁津县九年级上学期期末质量检测数学试卷(解析版) 题型:选择题
如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )

A.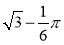 B.
B. C.
C.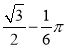 D.
D.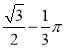
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省温州市泰顺县七年级上学期期中联考数学试卷(解析版) 题型:填空题
 如图,方格纸中的每一个小方格都是边长为1个单位长度的正方形,则图中阴影正方形的边长是________.
如图,方格纸中的每一个小方格都是边长为1个单位长度的正方形,则图中阴影正方形的边长是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com