
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图像经过点B、D.

(1)请直接写出用m表示点A、D的坐标;
(2)求这个二次函数的解析式;
(3)点Q为二次函数图像上点P至点B之间的一点,连结PQ、BQ,求四边形ABQP面积的最大值.
|
解:(1)A(3-m,0),D(0,m-3);2分 (2)设以P(1,0)为顶点的抛物线的解析式为y=a(x-1)2(a≠0) ∵抛物线过点B、D, ∴ 所以二次函数的解析式为y=(x-1)2, 即:y=x2-2x+1;5分 (3)设点Q的坐标为(x,x2-2x+1),显然1<x<3;6分 连结BP,过点Q作QH⊥x轴,交BP于点H. ∵A(-1,0),P(1,0),B(3,4) ∴AP=2,BC=3,PC=2 由P(1,0),B(3,4)求得直线BP的解析式为y=2x-2 ∵QH⊥x轴,点Q的坐标为(x,x2-2x+1) ∴点H的横坐标为x,∴点H的坐标为(x,2x-2) ∴QH=2x-2-(x2-2x+1)=-x2+4x-3;7分 ∴四边形ABQP面积S=S△APB+S△QPB= = =-x2+4x+1=-(x-2)2+5;9分 ∵1<x<3 ∴当x=2时,S取得最大值为5,10分 即当点Q的坐标为(2,1)时,四边形ABQP面积的最大值为5. 说明:用平行于PB的直线与抛物线相切于点Q的方法而得出准确结果不给全分(注:初中阶段没有解题依据),可统一扣1分.
|


科目:初中数学 来源: 题型:
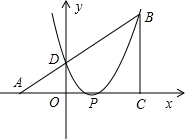 ,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.
,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:
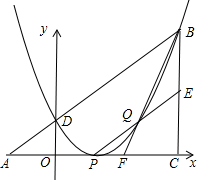 如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B、D.查看答案和解析>>
科目:初中数学 来源: 题型:
 25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.
25、如图,已知△ABC为等边三角形,D、F分别为BC、AB边上的点,CD=BF,以AD为边作等边△ADE.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.
如图,已知△ABC为等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.
如图,已知△ABC为等边三角形,点D.E分别在BC.AC边上,且AE=CD,AD与BE相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com