
在Rt△ABC中,∠BAC=90°,∠B=30°,线段AD是BC边上的中线.
(1)如图(Ⅰ),将△ADC沿直线BC平移,使点D与点C重合,得到△FCE,连结AF.
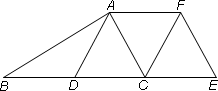
求证:四边形ADEF是等腰梯形;
(2)如图(Ⅱ),在(1)的条件下,再将△FCE绕点C顺时针旋转,设旋转角为α(0°<α<90°)连结AF、DE.

①当AC⊥CF时,求旋转角α的度数;②当α=60°时,请判断四边形ADEF的形状,并给予证明.
|
(1)证明:∵△ADC沿直线BC平移得到△FCE, ∴AD∥FC,且AD=FC,∴四边形ADCF是平行四边形, ∴AF∥DC,即AF∥DE, 1分 ∵∠BAC=90°,∠B=30°,∴∠ACD=60°, ∵AD是BC边上的中线,∴AD=DC, 2分 ∴△ADC是等边三角形, 3分 ∵△ADC≌△FCE,∴△FCE是等边三角形, ∴AD=FE, 4分 ∵AF≠DE,∴四边形ADEF是等腰梯形. 5分 (2)①解:由(1)可知∠1=60°, 6分 当AC⊥CF时,∠2=90°-60°=30°, ∴旋转角 ②四边形ADEF为矩形, 8分 由(1)可知△ADC和△FCE是全等正三角形, ∴CA=CE=CD=CF, 9分 当α=60°时,如图(Ⅲ),∠ACF=60°+60°=120°, ∴∠ACE=120°+60°=180°,∴A、C、E三点共线,同理:D、C、F三点共线, 10分 ∴AE=DF, 11分 ∴四边形ADEF为矩形. 12分 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com