
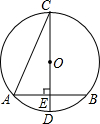
 如图,⊙O的直径CD垂直于弦AB,垂足为E,∠ACD=22.5°,CD=4.
如图,⊙O的直径CD垂直于弦AB,垂足为E,∠ACD=22.5°,CD=4.分析 (1)根据等边对等角可得∠OAC=∠OCA=22.5°,再根据三角形外角的性质可得∠COE=45°,进而求出AE的长,再根据垂径定理可得答案;
(2)求出CE的长,利用正切值的定义求出答案.
解答 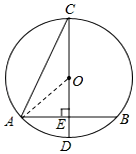 解:(1)连结OA.
解:(1)连结OA.
∵∠ACD=22.5°,
∴∠AOD=45°,
∵CD⊥AB,
∴∠AEO=90°,
∴AE=OE,
在Rt△AOE中,OA=2,
∴AE=OE=$\sqrt{2}$,
由垂径定理,得AB=2AE=2$\sqrt{2}$;
(2)∵CE=2+$\sqrt{2}$,AE=$\sqrt{2}$,
∴tan∠BAC=$\frac{CE}{AE}$=$\frac{2+\sqrt{2}}{\sqrt{2}}$=$\sqrt{2}$+1.
点评 此题主要考查了圆周角定理、垂径定理以及解直角三角形等知识,关键是掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:解答题
 国庆期间,林老师驾轿车从舟山出发,上高速途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到舟山.
国庆期间,林老师驾轿车从舟山出发,上高速途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速,其间用了4.5小时;返回时平均速度提高了10千米/小时,比去时少用了半小时回到舟山.| 大桥名称 | 舟山跨海大桥 | 杭州湾跨海大桥 |
| 大桥长度 | 48千米 | 36千米 |
| 过桥费 | 100元 | 80元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
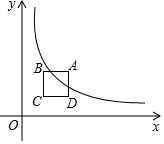 如图,在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),若双曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点.
如图,在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),若双曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5,12,13 | B. | 1,2,$\sqrt{5}$ | C. | 6,8,12 | D. | 3a,4a,5a(a>0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 66πcm2 | B. | 15πcm2 | C. | 28πcm2 | D. | 30πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com