
| x | 50 | 80 | 100 | 120 |
| y | 40 | 34 | 30 | 26 |
分析 (1)设y与x之间的函数关系式为y=kx+b,运用待定系数法就可以求出y与x之间的函数关系式;
(2)把x=70代入(1)中的函数解析式可得y的值.
解答 解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),由题意,得
$\left\{\begin{array}{l}{40=50k+b}\\{38=60k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{5}}\\{b=50}\end{array}\right.$,
∴y与x之间的函数关系式为:y=-$\frac{1}{5}$x+50(30≤x≤120);
(2)当x=70时,y=-$\frac{1}{5}$×70+50=36,
答:平均每天的修建费是36万元.
点评 本题考查了运用待定系数法求函数的解析式的运用,关键是掌握待定系数法求一次函数解析式的方法.


科目:初中数学 来源:2016-2017学年广东省揭阳市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
设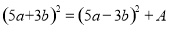 ,则A=( )
,则A=( )
A. 30ab B. 60ab C. 15ab D. 12ab
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | m | 0 | 2 |
| y1 | 4 | 3 | t |
| y2 | 6 | n | -1 |
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{2}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com