
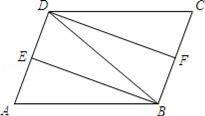
如图,在▱ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.

【考点】矩形的判定;全等三角形的判定与性质;平行四边形的性质.
【专题】证明题.
【分析】(1)根据平行四边形性质得出AB=CD,∠A=∠C.求出∠ABD=∠CDB.推出∠ABE=∠CDF,根据ASA推出全等即可;
(2)根据全等得出AE=CF,根据平行四边形性质得出AD∥BC,AD=BC,推出DE∥BF,DE=BF,得出四边形DFBE是平行四边形,根据等腰三角形性质得出∠DEB=90°,根据矩形的判定推出即可.
【解答】证明:(1)在□ABCD中,AB=CD,∠A=∠C.
∵AB∥CD,
∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=
 ∠ABD,∠CDF=
∠ABD,∠CDF=
 ∠CDB.
∠CDB.
∴∠ABE=∠CDF.
∵在△ABE和△CDF中,
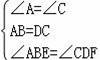

∴△ABE≌△CDF(ASA).
(2)∵△ABE≌△CDF,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE∥BF,DE=BF,
∴四边形DFBE是平行四边形,
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∴平行四边形DFBE是矩形.
【点评】本题考查了平行线的性质,平行四边形的性质和判定,矩形的判定,全等三角形的性质和判定,角平分线定义等知识点的应用,主要考查学生综合运用性质进行推理的能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2015年初中毕业升学考试(新疆生产建设兵团卷)数学(解析版) 题型:选择题
(5分)估算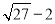 的值( )
的值( )
A.在1到2之间 B.在2到3之间 C.在3到4之间 D.在4到5之间
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=﹣
 ,下列结论不正确的是( )
,下列结论不正确的是( )
A.图象必经过点(﹣1,3)
B.两个分支分布在第二、四象限
C.若x>1,则﹣3<y<0
D.y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=2,BC=1,O是AB的中点,动点P从B点开始沿着边BC,CD运动到点D结束.设BP=x,OP=y,则y关于x的函数图象大致为( )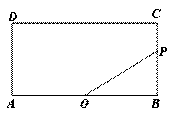
A.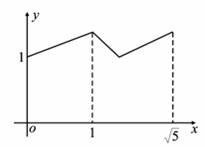 B.
B.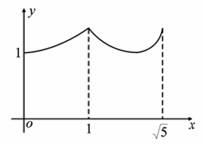
C.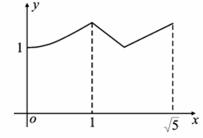 D.
D.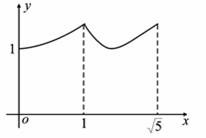
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线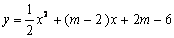 的对称轴为直线x=1,与x轴交于A,B 两点(点A在点B的左侧),与y轴交于点C.
的对称轴为直线x=1,与x轴交于A,B 两点(点A在点B的左侧),与y轴交于点C.
(1)求m的值;
(2)求A,B,C三点的坐标;
(3)过点C作直线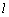 ∥x轴,将该抛物线在y轴左侧的部分沿直线
∥x轴,将该抛物线在y轴左侧的部分沿直线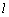 翻折,抛物线的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:
翻折,抛物线的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:
当直线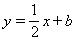 与图象G只有一个公共点时,求b的取值范围.
与图象G只有一个公共点时,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com