在Rt△ABC中,∠C=90°,AC=3,BC=4,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是( )
A.点P,M均在圆A内
B.点P、M均在圆A外
C.点P在圆A内,点M在圆A外
D.点P在圆A外,点M在圆A内
【答案】
分析:先利用勾股定理求得AB的长,再根据面积公式求出CP的长,根据勾股定理求出AP的长,根据中线的定义求出AM的长,然后由点P、M到A点的距离判断点P、M与圆A的位置关系即可.
解答:
解:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,
∴AB=
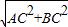
=5,
∵CP、CM分别是AB上的高和中线,
∴

AB•CP=

AC•BC,AM=

AB=2.5,
∴CP=
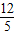
,
∴AP=
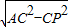
=1.8,
∵AP=1.8<2,AM=2.5>2,
∴点P在圆A内、点M在圆A外
故选C.
点评:本题考查了点与圆的位置关系的判定,根据点与圆心之间的距离和圆的半径的大小关系作出判断即可.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案