
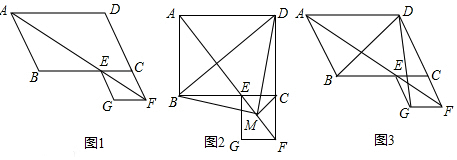
分析 (1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;
(2)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到∠BDM的度数;
(3)延长AB、FG交于H,连接HD,求证平行四边形AHFD为菱形,得出△ADH,△DHF为全等的等边三角形,证明△BHD≌△GFD,即可得出答案.
解答 解:(1)证明:如图1中,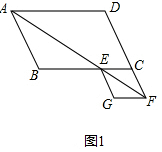
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形,
∴EG=GF.
(2)结论:△BMD是等腰直角三角形.
理由:如图2中,连接BM,MC,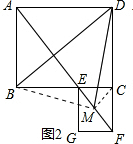
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵$\left\{\begin{array}{l}{BE=CD}\\{∠BEM=∠DCM}\\{EM=CM}\end{array}\right.$,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
(3)结论:∠BDG=60°,
如图3中,延长AB、FG交于H,连接HD.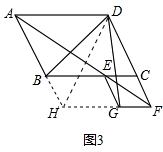
∵AD∥GF,AB∥DF,
∴四边形AHFD为平行四边形,
∵∠ABC=120°,AF平分∠BAD,
∴∠DAF=30°,∠ADC=120°,∠DFA=30°,
∴△DAF为等腰三角形,
∴AD=DF,
∴平行四边形AHFD为菱形,
∴△ADH,△DHF为全等的等边三角形,
∴DH=DF,∠BHD=∠GFD=60°,
∵FG=CE,CE=CF,CF=BH,
∴BH=GF,
在△BHD与△GFD中,
∵$\left\{\begin{array}{l}{DH=DF}\\{∠BHD=∠GFD}\\{BH=GF}\end{array}\right.$,
∴△BHD≌△GFD(SAS),
∴∠BDH=∠GDF
∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.
点评 此题主要考查平行四边形的判定方法,全等三角形的判定与性质,等边三角形的判定与性质,菱形的判定与性质等知识点,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
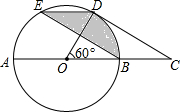 如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB. 若图中阴影部分面积为6π,则⊙O的半径为6.
如图,在⊙O中,AB是直径,点D是⊙O上一点,且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为弧AD的中点,连接DE,EB. 若图中阴影部分面积为6π,则⊙O的半径为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com