
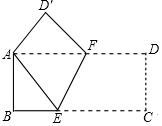
 按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长.
按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长. 分析 根据翻折变换的性质可得AE=CE,设BE=x,表示出AE,然后在Rt△ABE中,利用勾股定理列方程求解,即可得出BE长;再作EG⊥AD于G,根据勾股定理,即可得出折痕EF的长.
解答 解:∵矩形纸片ABCD折叠C点与A点重合,
∴AE=CE,
设BE=x,则AE=8-x=CE,
在Rt△ABE中,由勾股定理得,
AB2+BE2=AE2,
即32+x2=(9-x)2,
解得x=4,
即BE=4,AE=5.
如图,过点E作EG⊥AD于G,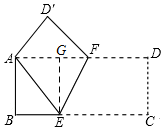
由折叠得,∠AEF=∠CEF,
又∵∠CEF=∠AFE,
∴∠AEF=∠AFE,
∴AE=AF=5,
∵∠B=∠BAG=∠AGE=90°,
∴四边形ABEG是矩形,
∴EG=AB=3,BE=AG=4,
∴GF=AF-AG=5-4=1,
∴Rt△EFG中,EF=$\sqrt{G{F}^{2}+E{G}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$.
点评 本题考查了翻折变换的性质,主要利用了翻折前后的重叠的边,重叠的角都相等,难点在于利用勾股定理列出方程.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
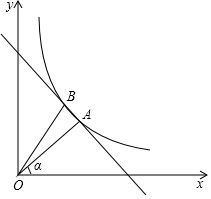 如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com