
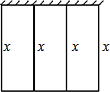
 周长为48m的篱笆,一面利用旧墙围成如图所示的矩形花圃:①写出花圃面积y与x的函数关系式;②给出x的取值范围;③求宽x为何值时,花圃的面积最大?
周长为48m的篱笆,一面利用旧墙围成如图所示的矩形花圃:①写出花圃面积y与x的函数关系式;②给出x的取值范围;③求宽x为何值时,花圃的面积最大?

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
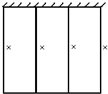 17、周长为48m的篱笆,一面利用旧墙围成如图所示的矩形花圃:①写出花圃面积y与x的函数关系式;②给出x的取值范围;③求宽x为何值时,花圃的面积最大?
17、周长为48m的篱笆,一面利用旧墙围成如图所示的矩形花圃:①写出花圃面积y与x的函数关系式;②给出x的取值范围;③求宽x为何值时,花圃的面积最大?查看答案和解析>>
科目:初中数学 来源:2008-2009学年广东省珠海市斗门区实验中学九年级(上)数学寒假作业(1)(解析版) 题型:解答题
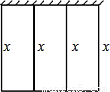
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com