
解:(1)把A(-4,4)代入y=kx+1得:
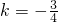
,
∴一次函数的解析式为

;
(2)由
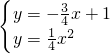
,
解得
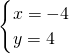
或
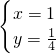
,
∴
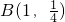
,
过A,B点分别作直线l的垂线,垂足为A',B',
则

,
∴直角梯形AA'B'B的中位线长为
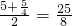
,
过B作BH垂直于直线AA'于点H,则BH=A'B'=5,
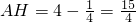
,
∴
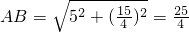
,
∴AB的长等于AB中点到直线l的距离的2倍,
∴以AB为直径的圆与直线l相切.
(3)(方法一) 平移后二次函数解析式为

,
令y=0,得

,

,
∵过F,M,N三点的圆的圆心一定在平移后抛物线的对称轴上,点C为定点,B要使圆面积最小,圆半径应等于点F到直线x=2的距离,
此时,半径为2,面积为4π,
设圆心为C,MN与直线x=2交于点E,连接CM,则CE⊥MN,ME=NE,CE=OF=1,
在直角三角形CEM中,

,
∴
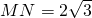
,而MN=|x
1-x
2|=

,从而求得
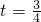
,
∴当
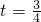
时,过F,M,N三点的圆面积最小;
(方法二) 设圆心为C,半径为r,
由

=0,得

,
∴ME=NE=2

则CE=

=

=

,
∴点C(2,

),
又F(0,1)∴由CF=r得:

,
整理得

,
∴当
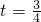
时,过F,M,N三点的圆面积最小.
分析:(1)已知了一次函数的图象经过A点,可将A点的坐标代入一次函数中,即可求出一次函数的解析式.
(2)求直线与圆的位置关系需知道圆心到直线的距离和圆的半径长.由于直线l平行于x轴,因此圆心到直线l的距离为1.因此只需求出圆的半径,也就是求AB的长,根据(1)中两函数的解析式即可求出B点的坐标,根据A、B两点的坐标即可求出AB的长.然后判定圆的半径与1的大小关系即可.
(3)先设出平移后抛物线的解析式,不难得出平移后抛物线的对称轴为x=2.因此过F,M,N三点的圆的圆心必在直线x=2上,要使圆的面积最小,那么圆心到F点的距离也要最小(设圆心为C),即F,C两点的纵坐标相同,因此圆的半径就是2.C点的坐标为(2,1)(可根据一次函数的解析式求出F点的坐标).可设出平移后的抛物线的解析式,表示出MN的长,如果设对称轴与x轴的交点为E,那么可表示出ME的长,然后在直角三角形MEC中根据勾股定理即可确定平移的距离.即t的值.(也可根据C点的坐标求出M,N点的坐标,然后用待定系数法求出平移后的抛物线的解析式,经过比较即可得出平移的距离,即t的值).
点评:此题主要考查了求一次函数解析式、二次函数的平移、勾股定理,二次函数的最值,直线与圆的位置关系,解二元二次方程组等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键,综合考查了学生数形结合的数学思想方法.

 的图象与一次函数y=kx+1的图象交于A,B两点(A在B的
的图象与一次函数y=kx+1的图象交于A,B两点(A在B的 左侧),且A点坐标为(-4,4).
左侧),且A点坐标为(-4,4). 解:(1)把A(-4,4)代入y=kx+1得:
解:(1)把A(-4,4)代入y=kx+1得: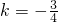 ,
, ;
;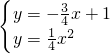 ,
,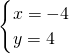 或
或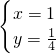 ,
,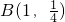 ,
, ,
,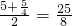 ,
,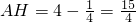 ,
,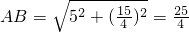 ,
, ,
, ,
, ,
, ,
,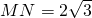 ,而MN=|x1-x2|=
,而MN=|x1-x2|= ,从而求得
,从而求得 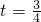 ,
,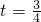 时,过F,M,N三点的圆面积最小;
时,过F,M,N三点的圆面积最小; =0,得
=0,得 ,
,
 =
= =
= ,
, ),
), ,
, ,
,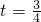 时,过F,M,N三点的圆面积最小.
时,过F,M,N三点的圆面积最小.

 已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.
已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.