
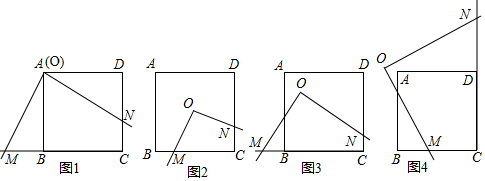
分析 (1)根据△OBM与△ODN全等,可以得出OM与ON相等的数量关系;
(2)连接AC、BD,则通过判定△BOM≌△CON,可以得到OM=ON;
(3)过点O作OE⊥BC,作OF⊥CD,可以通过判定△MOE≌△NOF,得出OE=OF,进而发现点O在∠C的平分线上;
(4)可以运用(3)中作辅助线的方法,判定三角形全等并得出结论.
解答 解:(1)若点O与点A重合,则OM与ON的数量关系是:OM=ON;
理由:∵四边形ABCD时正方形,
∴AB=AD,∠ADC=∠ABM=∠BAD=90°,
∵∠MON=90°,
∴∠BAM=∠DAN,
在△ABM和△ADN中,$\left\{\begin{array}{l}{∠BAM=∠DAN}\\{AB=AD}\\{∠ABM=∠ADN}\end{array}\right.$
∴△ABM≌△ADN,
∴OM=ON,
故答案为:OM=ON,
(2)仍成立.
证明:如图2,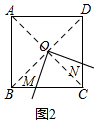 连接AC、BD,则
连接AC、BD,则
由正方形ABCD可得,∠BOC=90°,BO=CO,∠OBM=∠OCN=45°
∵∠MON=90°
∴∠BOM=∠CON
在△BOM和△CON中,$\left\{\begin{array}{l}{∠OBM=∠OCN}\\{BO=CO}\\{∠BOM=∠CON}\end{array}\right.$
∴△BOM≌△CON(ASA)
∴OM=ON
(3)如图3,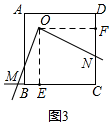 过点O作OE⊥BC,作OF⊥CD,垂足分别为E、F,则∠OEM=∠OFN=90°
过点O作OE⊥BC,作OF⊥CD,垂足分别为E、F,则∠OEM=∠OFN=90°
又∵∠C=90°
∴∠EOF=90°=∠MON
∴∠MOE=∠NOF
在△MOE和△NOF中,$\left\{\begin{array}{l}{∠OEM=∠OFN}\\{∠MOE=∠NOF}\\{OM=ON}\end{array}\right.$
∴△MOE≌△NOF(AAS)
∴OE=OF
又∵OE⊥BC,OF⊥CD
∴点O在∠C的平分线上,
∵点O在正方形的内部(含边界)
∴O在移动过程中可形成线段AC
(4)如图4,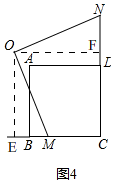 过点O作OE⊥BC,作OF⊥CD,垂足分别为E、F,则∠OEM=∠OFN=90°
过点O作OE⊥BC,作OF⊥CD,垂足分别为E、F,则∠OEM=∠OFN=90°
又∵∠C=90°
∴∠EOF=90°=∠MON
∴∠MOE=∠NOF
在△MOE和△NOF中,$\left\{\begin{array}{l}{∠OEM=∠OFN}\\{∠MOE=∠NOF}\\{OM=ON}\end{array}\right.$
∴△MOE≌△NOF(AAS)
∴OE=OF
又∵OE⊥BC,OF⊥CD
∴点O在∠C的平分线上,
∵点O在正方形外部,
∴O在移动过程中可形成直线AC中除去线段AC的部分.
点评 此题是四边形综合题,主要考查了正方形的性质全等三角形的判定和性质,解决问题的关键是作辅助线构造全等三角形.解题时需要运用全等三角形的判定与性质,以及角平分线的判定定理.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
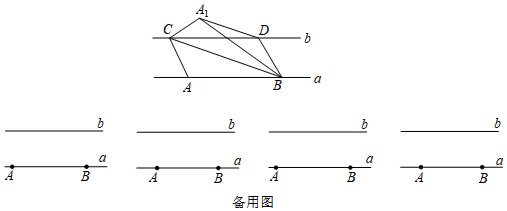
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
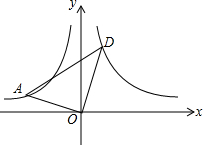 如图,∠AOB=90°,且点A,B分别在反比例函数y=$\frac{{k}_{1}}{x}$(x<0),y=$\frac{{k}_{2}}{x}$(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
如图,∠AOB=90°,且点A,B分别在反比例函数y=$\frac{{k}_{1}}{x}$(x<0),y=$\frac{{k}_{2}}{x}$(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
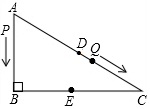 如图,在Rt△ABC中,∠B=90°,∠C=30°,AB=12厘米,点P从A出发沿线路AB-BC作匀速运动,点Q从AC的中点D同时出发沿线路DC-CB作匀速运动逐步靠近点P.设两点P、Q的速度分别为1厘米/秒、a厘米/秒(a>1),它们在t秒后于BC边上的某一点E相遇.
如图,在Rt△ABC中,∠B=90°,∠C=30°,AB=12厘米,点P从A出发沿线路AB-BC作匀速运动,点Q从AC的中点D同时出发沿线路DC-CB作匀速运动逐步靠近点P.设两点P、Q的速度分别为1厘米/秒、a厘米/秒(a>1),它们在t秒后于BC边上的某一点E相遇. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
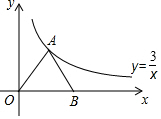 已知反比例函数y=$\frac{3}{x}$在第一象限的图象如图所示,点A是在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=3.
已知反比例函数y=$\frac{3}{x}$在第一象限的图象如图所示,点A是在其图象上,点B为x轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com