
分析 根据题意画出符合条件的两种情况,推出AP=BP,推出∠BAC=∠ABP,求出∠BAC的度数和∠ABC的度数即可.
解答 解:分为两种情况:
①如图1,
∵PE是AB的垂直平分线,
∴AP=BP,
∴∠A=∠ABP,∠APE=∠BPE=54°,
∴∠A=∠ABP=36°,
∵∠A=36°,AB=AC,
∴∠C=∠ABC=$\frac{1}{2}$(180°-∠A)=72°;
②如图2,
∵PE是AB的垂直平分线,
∴AP=BP,
∴∠PAB=∠ABP,∠APE=∠BPE=54°,
∴∠PAB=∠ABP=36°,
∴∠BAC=144°,
∵AB=AC,
∴∠C=∠ABC=$\frac{1}{2}$(180°-∠A)=18°,
故答案为:72°或18°.
点评 本题考查了线段垂直平分线性质,等腰三角形的性质和判定,三角形的内角和定理等知识点,主要考查学生分析问题和解决问题的能力,注意:符合条件的有两种情况.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
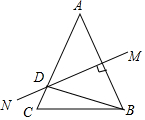 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )
如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是( )| A. | 50° | B. | 45° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com