
分析 (1)根据不可能事件的定义,x为小于2的正整数即可;
(2)画树状图展示所有12种等可能的结果数,再找出摸出两枚棋子的颜色相同的结果数和摸出两枚棋子的颜色不同的结果数,然后根据概率公式计算后可判定它们的概率是否相等.
解答 解:(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,则x为1或0;
故答案为1(或0);
(2)不相等.理由如下:
画树状图为: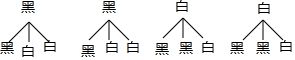
共有12种等可能的结果数,其中摸出两枚棋子的颜色相同的结果数为4,摸出两枚棋子的颜色不同的结果数为8,
所以摸出两枚棋子的颜色相同的概率=$\frac{4}{12}$=$\frac{1}{3}$,摸出两枚棋子的颜色不同的概率=$\frac{8}{12}$=$\frac{2}{3}$,
所以“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率不相等.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.\


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
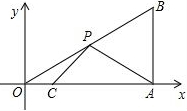 如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.
如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的纵坐标为2$\sqrt{3}$,∠B=60°,OC=$\frac{1}{2}$AC,点P是斜边DB上的一个动点,则△PAC的周长的最小值为2$\sqrt{7}$+4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
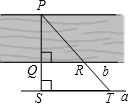 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )
如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P、Q、S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )| A. | 40m | B. | 120m | C. | 60m | D. | 180m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com