
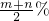 .若m>n>0,则提价最多的方案是
.若m>n>0,则提价最多的方案是 %)2显然甲、乙两种方案最终价格是一致的,因而只需比较(1+m%)(1+n%)与(1+
%)2显然甲、乙两种方案最终价格是一致的,因而只需比较(1+m%)(1+n%)与(1+ %)2的大小.
%)2的大小. %)2=1+(m+n)%+(
%)2=1+(m+n)%+( % )2;
% )2; %)2的大小即可
%)2的大小即可 %)2-m%•n%≥0
%)2-m%•n%≥0 %)2≥m%•n%
%)2≥m%•n% %)2>(1+m%) (1+n%)
%)2>(1+m%) (1+n%)

科目:初中数学 来源: 题型:
| m+n |
| 2 |
| A、甲 | B、乙 | C、丙 | D、无法确定 |
查看答案和解析>>
科目:初中数学 来源:期中题 题型:单选题
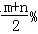 .若m>n>0,则提价最多的方案是
.若m>n>0,则提价最多的方案是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com