
【题目】在平面直角坐标系中,已知反比例函数y= ![]() 的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°. 
(1)试确定此反比例函数的解析式;
(2)将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
【答案】
(1)解:作AC⊥x轴于点C,如图:
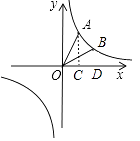
在Rt△AOC中,
∵OA=2,∠AOC=60°,
∴∠OAC=30°,
∴OC= ![]() OA=1,AC=
OA=1,AC= ![]() OC=
OC= ![]() ,
,
∴A点坐标为(1, ![]() ),
),
把A(1, ![]() )代入y=
)代入y= ![]() ,
,
得k=1× ![]() =
= ![]() ,
,
∴反比例函数的解析式为y= ![]() ;
;
(2)解:点B在此反比例函数的图象上,
理由如下:过点B作x轴的垂线交x轴于点D,
∵线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,∴∠BOD=30°,
在Rt△BOD中,BD= ![]() OB=1,OD=
OB=1,OD= ![]() BD=
BD= ![]() ,
,
∴B点坐标为( ![]() ,1),
,1),
∵当x= ![]() 时,y=
时,y= ![]() =1,
=1,
∴点B( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.
【解析】(1)作AC⊥x轴于点C,在Rt△AOC中,解直角三角形求得A点坐标为(1, ![]() ),把A(1,
),把A(1, ![]() )分别代入代入y=
)分别代入代入y= ![]() ,根据待定系数法即可求得;(2)作BD⊥x轴于点D,在Rt△BOD中,解直角三角形求得B点坐标为(
,根据待定系数法即可求得;(2)作BD⊥x轴于点D,在Rt△BOD中,解直角三角形求得B点坐标为( ![]() ,1),把x=
,1),把x= ![]() 代入代入y=
代入代入y= ![]() ,即可判断.
,即可判断.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读题.
材料一:若一个整数m能表示成a2-b2(a,b为整数)的形式,则称这个数为“完美数”.例如,3=22-12,9=32-02,12=42-22,则3,9,12都是“完美数”;再如,M=x2+2xy=(x+y)2-y2,(x,y是整数),所以M也是”完美数”.
材料二:任何一个正整数n都可以进行这样的分解:n=p×q(p、q是正整数,且p≤q).如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并且规定F(n)=![]() .例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=
.例如18=1×18=2×9=3×6,这三种分解中3和6的差的绝对值最小,所以就有F(18)=![]() .请解答下列问题:
.请解答下列问题:
(1)8______(填写“是”或“不是”)一个完美数,F(8)= ______.
(2)如果m和n都是”完美数”,试说明mn也是完美数”.
(3)若一个两位数n的十位数和个位数分别为x,y(1≤x≤9),n为“完美数”且x+y能够被8整除,求F(n)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 到直线
到直线![]() 的距离分别为1,2.
的距离分别为1,2.
(1)利用直尺和圆规作出以![]() 为底的等腰△ABC,使点
为底的等腰△ABC,使点![]() 在直线
在直线![]() 上(保留作图痕迹,不写作法).
上(保留作图痕迹,不写作法).
(2)若(1)中得到的△ABC为等腰直角三角形,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.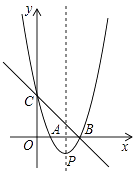
(1)求该抛物线的解析式;
(2)连接AC,在x轴上是否存在点Q,使以P、B、Q为顶点的三角形与△ABC相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),二次函数图象对称轴为x=1,给出四个结论:①b2>4ac;②bc<0;③2a+b=0;④a+b+c=0,其中正确结论是( )
A.②④
B.①③
C.②③
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A1B1C1关于直线l对称,将△A1B1C1向右平移得到△A2B2C2,由此得出下列判断:①∠A=∠A2;②A1B1=A2B2;③AB∥A2B2.其中正确的是( )
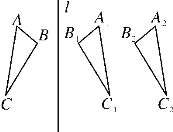
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com