
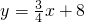 ,与x轴、y轴分别交于A、B两点,P是x轴上一点,以P为圆心的圆与直线l相切于B点.
,与x轴、y轴分别交于A、B两点,P是x轴上一点,以P为圆心的圆与直线l相切于B点. 个单位沿x轴向左运动,同时⊙P的半径以每秒
个单位沿x轴向左运动,同时⊙P的半径以每秒 个单位变小,设⊙P的运动时间为t秒,且⊙P始终与直线l有交点,试求t的取值范围;
个单位变小,设⊙P的运动时间为t秒,且⊙P始终与直线l有交点,试求t的取值范围; t的值.
t的值.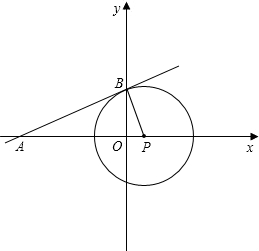 解:(1)如图,由于直线ly=
解:(1)如图,由于直线ly= +8与x轴、y轴分别交于A、B两点,
+8与x轴、y轴分别交于A、B两点, x+8,
x+8, .A(-
.A(- ,0),
,0), =
=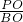 ,
,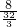 =
=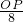 ,
, =10;
=10;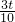 ),0],R=10-
),0],R=10- ,L:3x-4y+32=0,
,L:3x-4y+32=0,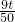 |,
|, ≥|10-
≥|10-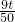 |,
|, ≥10-
≥10-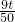 ≥-(10-
≥-(10- ),
), ≥10-2t≥-(10-
≥10-2t≥-(10- ),
), )2=R2-H2=(10-
)2=R2-H2=(10- )2-(10-2t)2=(-
)2-(10-2t)2=(- )×(t-
)×(t- )2+50,
)2+50, ,(
,(  )2最大=50,a最大=10
)2最大=50,a最大=10  ;
; +8,与x轴、y轴分别交于A、B两点,求出A(-
+8,与x轴、y轴分别交于A、B两点,求出A(- ,0),B(0,8),再得出△ABO∽△BPO,进而求出OP的长,再利用勾股定理求出即可.
,0),B(0,8),再得出△ABO∽△BPO,进而求出OP的长,再利用勾股定理求出即可.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
 平面直角坐标系内有两条直线l1、l2,直线l1的解析式为y=-
平面直角坐标系内有两条直线l1、l2,直线l1的解析式为y=-| 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
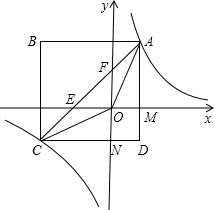 如图,矩形ABCD(点A在第一象限)与x轴的正半轴相交于M,与y的负半轴相交于N,AB∥x轴,反比例函数的图象y=
如图,矩形ABCD(点A在第一象限)与x轴的正半轴相交于M,与y的负半轴相交于N,AB∥x轴,反比例函数的图象y=| k | x |
查看答案和解析>>
科目:初中数学 来源:2006年湖北省孝感市汉川市中考数学试卷(解析版) 题型:解答题
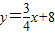 ,与x轴、y轴分别交于A、B两点,P是x轴上一点,以P为圆心的圆与直线l相切于B点.
,与x轴、y轴分别交于A、B两点,P是x轴上一点,以P为圆心的圆与直线l相切于B点.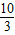 个单位沿x轴向左运动,同时⊙P的半径以每秒
个单位沿x轴向左运动,同时⊙P的半径以每秒 个单位变小,设⊙P的运动时间为t秒,且⊙P始终与直线l有交点,试求t的取值范围;
个单位变小,设⊙P的运动时间为t秒,且⊙P始终与直线l有交点,试求t的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
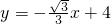 ,与x轴、y轴分别交于A、B两点,以线段AB为
,与x轴、y轴分别交于A、B两点,以线段AB为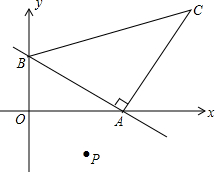 直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,在坐标平面内有一点P(a,2),且△ABP的面积与△ABC的面积相等.
直角边在第一象限内作等腰Rt△ABC,∠BAC=90°,在坐标平面内有一点P(a,2),且△ABP的面积与△ABC的面积相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com