
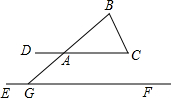
 如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是
如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
 如图,已知BC∥EF,BC=EF,AF=DC.则AB=DE.在相应序号内说明理由.
如图,已知BC∥EF,BC=EF,AF=DC.则AB=DE.在相应序号内说明理由.
|
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建福安溪潭中学七年级下期期末考试数学试卷(带解析) 题型:解答题
如图,已知BC∥EF,BC=EF,AF=DC.则AB=DE.在相应序号内说明理由.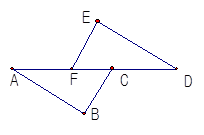
解:∵BC∥EF (已知)
∴∠BCA=∠EFD( ⑴ )
∵AF=DC(已知)
∴AF+FC=DC+FC
即 ⑵
在△ABC和△DEF中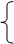 BC=EF( 已知 )
BC=EF( 已知 )
∠BCA=∠EFD (已证)
AC=DF(已证)
∴△ABC≌△DEF( ⑶ )
∴AB=DE( ⑷ )
查看答案和解析>>
科目:初中数学 来源:2014届福建福安溪潭中学七年级下期期末考试数学试卷(解析版) 题型:解答题
如图,已知BC∥EF,BC=EF,AF=DC.则AB=DE.在相应序号内说明理由.
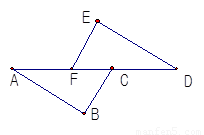
解:∵BC∥EF (已知)
∴∠BCA=∠EFD( ⑴ )
∵AF=DC(已知)
∴AF+FC=DC+FC
即 ⑵
在△ABC和△DEF中
 BC=EF( 已知 )
BC=EF( 已知 )
∠BCA=∠EFD (已证)
AC=DF(已证)
∴△ABC≌△DEF( ⑶ )
∴AB=DE( ⑷ )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com