解:(1)∵2x
2-x+4=2(x
2-

x)+4=2(x
2-

x+

)+4-

=2(x-

)
2+

,
∴当x=

时,2x
2-x+4有最小值,最小值为

,
则分式
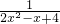
的最大值为
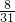
;
(2)∵分式
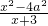
的值为0,
∴
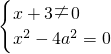
,解得x=±2a,且x≠-3,
则x的值为x=±2a,且x≠-3;
(3)

,
方程两边同时乘以最简公分母x(x-1)得:
x(x-a)-3(x-1)=x(x-1),
x
2-ax-3x+3=x
2-x,
整理得:(2+a)x=3,
解得:x=
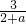
,
∵此分式方程无解,∴x=0或1,
若
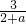
无意义,即a=-2,方程无解;
若
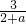
=1,解得:a=1,方程无解,
则a=-2或1时,原方程无解;
(4)
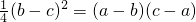
两边同时加上bc得:
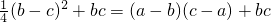
,
化简得:4a
2-4a(b+c)+(b+c)
2=0,
由a≠0,两边同时除以a
2得:
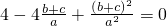
,
即
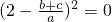
,
所以
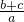
=2.
故答案为:
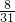
;x=±2a,且x≠-3;-2或1;2
分析:(1)将分式的分母配方后,根据完全平方式的最小值为0,求出分母的最小值,即可得到原式的最大值;
(2)根据分式值为0的条件是分母不为0,分子等于0,即可得到x的值;
(3)找出分式方程的最简公分母,去分母转化为整式方程,求出x的值,由原方程无解,得到分式方程的最简公分母为0,求出分式方程最简公分母为0时x的值,令其值等于表示出的x的解即可得到a的值,再由表示出的x的值无意义可得此时a的值,综上,即可得到原方程无解时a的值;
(4)根据题意利用添项法在原式两边同时加上bc,整理后,根据a不为0,在方程两边同时除以a
2后,等式可化为完全平方式等于0的形式,利用完全平方式的非负性,即可得到平方的底数为0,得出答案.
点评:此题考查了配方法的应用,分式值为0满足的条件,分式方程无解的条件,以及分式的化简求值,是一道多知识点的综合题,要求学生掌握知识要全面系统,灵活运用所学知识解决问题.本题的第4小题技巧性比较强,两边同时加上bc,然后在等式两边同时除以a
2,把等式变为完全平方式等于0是解题的关键.

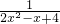 的最大值为______.
的最大值为______.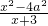 的值为0,则x的值为______.
的值为0,则x的值为______. 无解,则a的值为______.
无解,则a的值为______.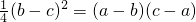 且a≠0,则
且a≠0,则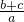 的值为______.
的值为______. x)+4=2(x2-
x)+4=2(x2- x+
x+ )+4-
)+4- =2(x-
=2(x- )2+
)2+ ,
, 时,2x2-x+4有最小值,最小值为
时,2x2-x+4有最小值,最小值为 ,
,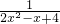 的最大值为
的最大值为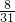 ;
;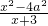 的值为0,
的值为0,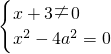 ,解得x=±2a,且x≠-3,
,解得x=±2a,且x≠-3, ,
,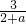 ,
,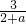 无意义,即a=-2,方程无解;
无意义,即a=-2,方程无解;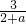 =1,解得:a=1,方程无解,
=1,解得:a=1,方程无解,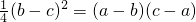
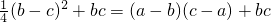 ,
,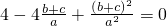 ,
,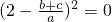 ,
,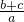 =2.
=2.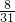 ;x=±2a,且x≠-3;-2或1;2
;x=±2a,且x≠-3;-2或1;2

![]() 一个整式与另一个分式的和(或差)的形式
一个整式与另一个分式的和(或差)的形式![]() ,其中另一个分式的分子次数低于分母次数.
,其中另一个分式的分子次数低于分母次数.![]() 如: .
如: .![]()
![]() 材料2:对于式子
材料2:对于式子![]() ,因为 ≥ ,所以
,因为 ≥ ,所以![]() 的最小值为1,所以
的最小值为1,所以![]() 的最
的最![]() 的最大值为5.根据上述材料,解决下列问题:
的最大值为5.根据上述材料,解决下列问题: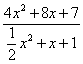 问题1
问题1![]() :把分式 化为一个整式与另一个分式的和(或差)的形式,其中另一
:把分式 化为一个整式与另一个分式的和(或差)的形式,其中另一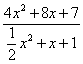 个分式的分子次数低于分母次数.
个分式的分子次数低于分母次数. =
=
 ,因为x2≥0,所以1+x2的最小值为1,所以
,因为x2≥0,所以1+x2的最小值为1,所以 的最大值为3,所以
的最大值为3,所以 的最大值为5.根据上述材料,解决下列问题:问题1:把分式
的最大值为5.根据上述材料,解决下列问题:问题1:把分式 化为一个整式与另一个分式的和(或差)的形式,其中另一
化为一个整式与另一个分式的和(或差)的形式,其中另一 个分式的分子次数低于分母次数.
个分式的分子次数低于分母次数. 的最小值.
的最小值.