
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

【答案】(1))AB是⊙O切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)结论:AB是⊙O切线,连接DE,CF,由∠FCD+∠CDF=90°,只要证明∠ADF=∠DCF即可解决问题.
(2)只要证明△PCF∽△PAC,得![]() ,设PF=a.则PC=2a,列出方程即可解决问题.
,设PF=a.则PC=2a,列出方程即可解决问题.
试题解析:(1)AB是⊙O切线.
理由:连接DE、CF.

∵CD是直径,
∴∠DEC=∠DFC=90°,
∵∠ACB=90°,
∴∠DEC+∠ACE=180°,
∴DE∥AC,
∴∠DEA=∠EAC=∠DCF,
∵∠DFC=90°,
∴∠FCD+∠CDF=90°,
∵∠ADF=∠EAC=∠DCF,
∴∠ADF+∠CDF=90°,
∴∠ADC=90°,
∴CD⊥AD,
∴AB是⊙O切线.
(2)∵∠CPF=∠CPA,∠PCF=∠PAC,
∴△PCF∽△PAC,
∴![]() ,
,
∴PC2=PFPA,设PF=a.则PC=2a,
∴4a2=a(a+5),
∴a=![]() ,
,
∴PC=2a=![]() .
.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】2014年3月28日是全国中小学安全教育日,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列统计图(说明:A级:90分--100分;B级:75分--89分;C级:60分--74分;D级:60分以下).请结合图中提供的信息,解答下列问题:

(1)扇形统计图中C级所在的扇形的圆心角度数是 ;
(2)请把条形统计图补充完整;
(3)若该校共有2000名学生,请你用此样本估计安全知识竞赛中A级和B级的学生共约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,∠ACB=90°,CD为高,且CD、CE三等分∠ACB.
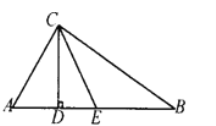
(1)求∠B的度数.
(2)求证:CE是AB边上的中线,且![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用尺规作一个直角三角形,使其两条直角边分别等于已知线段时,实际上就是已知的条件是( )
A. 三角形的两条边和它们的夹角
B. 三角形的三边
C. 三角形的两个角和它们的夹边
D. 三角形的三个角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面几种图形:①三角形;②长方形;③正方体;④圆;⑤圆锥;⑥圆柱.其中属于立体图形的是( )
A. ③⑤⑥ B. ①②③ C. ③⑥ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
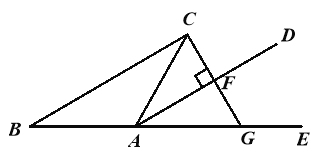
(1)求证:AD∥BC;
(2)过点C作CG⊥AD于点F,交AE于点G.若AF=4,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com