Question

16．如图，在Rt△ABC中，∠BAC=30°，以直角边AB为直径作半圆交AC于点D，以AD为边作等边△ADE，延长ED交BC于点F，BC=2$\sqrt{3}$，则图中阴影部分的面积为3$\sqrt{3}$-$\frac{3}{2}$π．（结果不取近似值）

Answer 1

分析 根据题意结合等边三角形的性质分别得出AB，AC，AD，DC的长，进而利用S_阴影=S_△ABC-S_△AOD-S_扇形DOB-S_△DCF求出答案．

解答 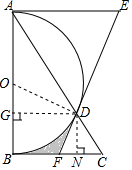解：如图所示：设半圆的圆心为O，连接DO，过D作DG⊥AB于点G，过D作DN⊥CB于点N，
∵在Rt△ABC中，∠BAC=30°，
∴∠ACB=60°，∠ABC=90°，
∵以AD为边作等边△ADE，
∴∠EAD=60°，
∴∠EAB=60°+30°=90°，
可得：AE∥BC，
则△ADE∽△CDF，
∴△CDF是等边三角形，
∵在Rt△ABC中，∠BAC=30°，BC=2$\sqrt{3}$，
∴AC=4$\sqrt{3}$，AB=6，∠DOG=60°，
则AO=BO=3，
故DG=DO•sin60°=$\frac{3\sqrt{3}}{2}$，
则AD=3$\sqrt{3}$，DC=AC-AD=$\sqrt{3}$，
故DN=DC•sin60°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$，
则S_阴影=S_△ABC-S_△AOD-S_扇形DOB-S_△DCF
=$\frac{1}{2}$×2$\sqrt{3}$×6-$\frac{1}{2}$×3×$\frac{3\sqrt{3}}{2}$-$\frac{60π×{3}^{2}}{360}$-$\frac{1}{2}$×$\frac{3}{2}$×$\sqrt{3}$
=3$\sqrt{3}$-$\frac{3}{2}$π．
故答案为：3$\sqrt{3}$-$\frac{3}{2}$π．

点评 此题主要考查了扇形面积求法以及等边三角形的性质和锐角三角函数关系等知识，正确分割图形是解题关键．