
如图所示,平面直角坐标系中,抛物线y=ax2+bx+c经过A(0,4)、B(-2,0)、C(6,0).过点A作AD∥x轴交抛物线于点D,过点D作DE⊥x轴,垂足为点E点M是四边形OADE的对角线的交点,点F在y轴负半轴上,且F(0,-2).
(1)求抛物线的解析式,并直接写出四边形OADE的形状;
(2)当点P、Q从C、F两点同时出发,均以每秒1个长度单位的速度沿CB、FA方向
运动,点P运动到O时P、Q两点同时停止运动.设运动的时间为t秒,在运动过
程中,以P、Q、O、M四点为顶点的四边形的面积为S,求出S与t之间的函数关
系式,并写出自变量的取值范围;
(3)在抛物线上是否存在点N,使以B、C、F、N为顶点的四边形是梯形?若存在,直
接写出点N的坐标;不存在,说明理由。
 | |||
 | |||
|
解:(1)∵抛物线经过A(0,4)、B(-2,0)、C(6,0)
![]()

解得a=-![]() ,b=
,b=![]() ,c=4(或可用交点式求解)
,c=4(或可用交点式求解)

![]() 抛物线的解析式为y=-
抛物线的解析式为y=-![]() x2+
x2+![]() x+4
x+4
(或y=-![]() (x+2)(x-6)或y=-
(x+2)(x-6)或y=-![]() (x-2)2 +
(x-2)2 +![]() .)
.)
四边形OADE为正方形.
(2)根据题意可知OE=OA=4,OC=6,OB=OF=2
∴CE=2 ∴CO=FA=6
∵运动的时间为t
∴CP=FQ=t
 过M作MN⊥OE于N,
过M作MN⊥OE于N,
则MN=2
当0≤t<2时,OP=6-t,OQ=2-t
∴S=![]() +
+![]() =
=![]() (6-t)×2+
(6-t)×2+![]() (6-t)
(6-t)
(2- t)=![]() (6-t)(4-t) ∴S =
(6-t)(4-t) ∴S =![]() t2-5t+12.
t2-5t+12.
当t=2时,Q与O重合,点M、O、P、Q不能构成四边形.
(不写也可)
当2<t<6时,连接MO,ME则MO=ME且∠QOM=∠PEM=45
∵FQ=CP=t,FO=CE=2 ∴OQ=EP
∴△QOM≌△PEM
∴四边形OPMQ的面积S=![]() =
=![]() ×4×2=4
×4×2=4
综上所述,当0≤t<2时,
S=![]() t
t![]() -5t+12;当2<t<6时, S=4
-5t+12;当2<t<6时, S=4
(3)存在N![]() (1,5),N
(1,5),N![]() (5,
(5,![]() ),
),
N![]() (2+
(2+![]() ,-2),N
,-2),N![]() (2-
(2-![]() ,-2)
,-2)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:059
学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图)

(1)按照这种规定填写下表:
(2)根据表中的数据,将s作为纵坐标,n作为横坐标,在如图所示的平面直角坐标系中找出相应各点.

(3)请你猜一猜上述各点会在某一个函数图象上吗?如果在某一函数图象上,求出该函数的解析式,并利用你探求的结果,求出当n=10时,s的值.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山西省九年级上学期期末考试数学试卷(解析版) 题型:解答题
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C( ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。
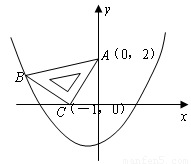
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:专项题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com