
 如图,在△ABC中,分别以点A和点B为圆心,大于
如图,在△ABC中,分别以点A和点B为圆心,大于| 1 |
| 2 |
| 1 |
| 2 |


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
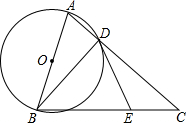 如图,在△ABC中,AC=BC,以AB为直径的⊙O交AC边于点D,点E在BC上,连结BD,DE,∠CDE=∠ABD.
如图,在△ABC中,AC=BC,以AB为直径的⊙O交AC边于点D,点E在BC上,连结BD,DE,∠CDE=∠ABD.| 5 |
| 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
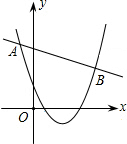 如图,已知二次函数y=ax2+bx+c(a>0)与一次函数y=kx+m的图象相交于A(-1,4)、B(6,3)两点,则能使关于x的不等式ax2+bx+c>kx+m成立的x的取值范围是( )
如图,已知二次函数y=ax2+bx+c(a>0)与一次函数y=kx+m的图象相交于A(-1,4)、B(6,3)两点,则能使关于x的不等式ax2+bx+c>kx+m成立的x的取值范围是( )| A、x<-1 |
| B、-1<x<6 |
| C、x>6 |
| D、x<-1或x>6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,双曲线y=
如图,双曲线y=| k |
| x |
| A、12 | B、24 | C、5 | D、10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
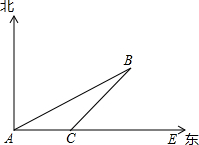 如图,一艘轮船由西向东航行,在A处测得小岛B在北偏东75°方向,又航行8海里后,在C处测得小岛B在北偏东60°方向,若小岛周围3.8海里范围内有暗礁,则该船一直向东航行有无触礁危险?
如图,一艘轮船由西向东航行,在A处测得小岛B在北偏东75°方向,又航行8海里后,在C处测得小岛B在北偏东60°方向,若小岛周围3.8海里范围内有暗礁,则该船一直向东航行有无触礁危险?查看答案和解析>>
科目:初中数学 来源: 题型:
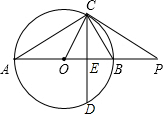 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠COB=2∠PCB.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com