
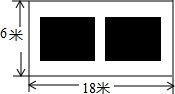
 某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度.
某小区在绿化工程中有一块长为18m、宽为6m的矩形空地,计划在其中修建两块相同的矩形绿地,使它们的面积之和为60m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),求人行通道的宽度. 科目:初中数学 来源: 题型:解答题
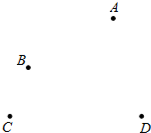 如图,平面上四个点A,B,C,D.按要求完成下列问题:
如图,平面上四个点A,B,C,D.按要求完成下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
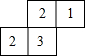 由若干个小正方形搭成几何体,从上面看到的几何体的形状如图所示,其中小方格中的数字表示在该位置的小正方体的个数,请在指定位置画出该几何体从正面看和从左面看得到的几何体的形状图.
由若干个小正方形搭成几何体,从上面看到的几何体的形状如图所示,其中小方格中的数字表示在该位置的小正方体的个数,请在指定位置画出该几何体从正面看和从左面看得到的几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
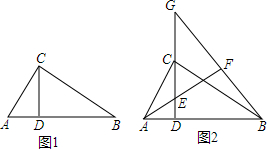 如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D;
如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com