
分析 先变形为|7-3m|+(n-5)2+2$\sqrt{m-3}$=3m-7,根据非负数的性质可得3m-7≥0,计算绝对值可得(n-5)2+2$\sqrt{m-3}$=0,再根据非负数的性质得到m,n的值,再代入计算即可求解.
解答 解:|7-3m|+(n-5)2=3m-7-2$\sqrt{m-3}$,
|7-3m|+(n-5)2+2$\sqrt{m-3}$=3m-7,
则3m-7≥0,
3m-7+(n-5)2+2$\sqrt{m-3}$=3m-7,
(n-5)2+2$\sqrt{m-3}$=0,
则n-5=0,m-3=0,
解得n=5,m=3,
则m-n=3-5=-2.
点评 本题考查了非负数的性质,关键是熟悉几个非负数的和为0时,这几个非负数都为0.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
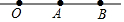 如图,O,A,B三点在同一直线上,则下列说法中正确的是( )
如图,O,A,B三点在同一直线上,则下列说法中正确的是( )| A. | 射线OA与射线AO表示同一条射线 | B. | 射线OA大于射线AB | ||
| C. | 射线OA与射线OB表示同一条射线 | D. | 线段OA与线段AO表示两条不同线段 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
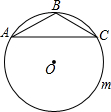 如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
如图,△ABC中,AB=BC,∠ABC=120°,AC=2$\sqrt{3}$,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )| A. | y=$\frac{\sqrt{3}}{4}$x+4 | B. | y=$\sqrt{3}$x+4 | C. | y=$\sqrt{3}$x2+4 | D. | y=$\frac{\sqrt{3}}{4}$x2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | B. | $\frac{x+1}{{x}^{2}-1}$ | ||
| C. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}-36}{2x+12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com