
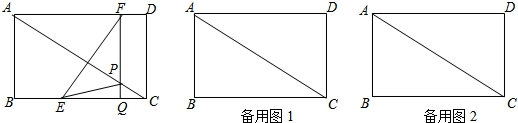
分析 (1)通过计算发现EQ=FQ=6,由此即可证明;
(2)构建二次函数,解方程即可得到结论;
(3)分两种情形讨论,Ⅰ、如图1中,点E在Q的左侧.①当△EPQ∽△ACD时,②当△EPQ∽△CAD时,列出方程分别求解即可.Ⅱ、如图2中,点E在Q的右侧,只存在△EPQ∽△CAD列出方程即可解决.
解答  (1)证明:若运动时间t=$\frac{2}{3}$秒,则
(1)证明:若运动时间t=$\frac{2}{3}$秒,则
BE=2×$\frac{2}{3}$=$\frac{4}{3}$(cm),DF=$\frac{2}{3}$(cm),
∵四边形ABCD是矩形
∴AD=BC=8(cm),AB=DC=6(cm),∠D=∠BCD=90°
∵∠D=∠FQC=∠QCD=90°,
∴四边形CDFQ也是矩形,
∴CQ=DF,CD=QF=6(cm),
∴EQ=BC-BE-CQ=8-$\frac{4}{3}$-$\frac{2}{3}$=6(cm),
∴EQ=QF=6(cm),
又∵FQ⊥BC,
∴△EQF是等腰直角三角形,
(2)解:∵∠FQC=90°,∠B=90°,
∴∠FQC=∠B,
∴PQ∥AB,
∴△CPQ∽△CAB,
∴$\frac{PQ}{AB}$=$\frac{QC}{BC}$,
即$\frac{PQ}{6}$=$\frac{t}{8}$,
∴PQ=$\frac{3}{4}$t,
∵S△EPC=$\frac{1}{2}$•EC•PQ,
∴S=$\frac{1}{2}$(8-2t)•$\frac{3}{4}$t=-$\frac{3}{4}$t2+3t
当S=3时,-$\frac{3}{4}$t2+3t=3,
解之得:t1=t2=2∴当S=3时t的值为2
(3)解:分两种情况讨论:
Ⅰ.如图1中,点E在Q的左侧.
①当△EPQ∽△ACD时,
可得$\frac{PQ}{CD}=\frac{EQ}{AD}$,即$\frac{\frac{3}{4}t}{6}$=$\frac{8-3t}{8}$,解得 t=2.
②当△EPQ∽△CAD时,
可得$\frac{PQ}{CD}$=$\frac{EQ}{CD}$,即$\frac{\frac{3}{4}t}{8}$=$\frac{8-3t}{6}$,解得t=$\frac{128}{57}$.
Ⅱ.如图2中,点E在Q的右侧.
∵0<t<4,
∴点E不能与点C重合,
∴只存在△EPQ∽△CAD
可得$\frac{PQ}{AD}$=$\frac{EQ}{CD}$,即$\frac{\frac{3}{4}t}{8}$=$\frac{3t-8}{6}$,解得t=$\frac{128}{39}$,
故若△EPQ与△ADC相似,则t的值为2或$\frac{128}{57}$或$\frac{128}{39}$.
点评 本题考查相似三角形的判定和性质、等腰三角形的性质、二次函数的性质、矩形的性质等知识,解题的关键是利用相似三角形的性质,把问题转化为方程解决,学会分类讨论的思想,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
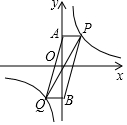 反比例函数y=$\frac{a+4}{x}$的图象如图所示,P、Q为该图象上关于原点对称的两点,分别过点P、Q作y轴的垂线,垂足分别为A、B.若四边形AQBP的面积大于12,则关于x的方程(a-1)x2-x+$\frac{1}{4}$=0的根的情况是( )
反比例函数y=$\frac{a+4}{x}$的图象如图所示,P、Q为该图象上关于原点对称的两点,分别过点P、Q作y轴的垂线,垂足分别为A、B.若四边形AQBP的面积大于12,则关于x的方程(a-1)x2-x+$\frac{1}{4}$=0的根的情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
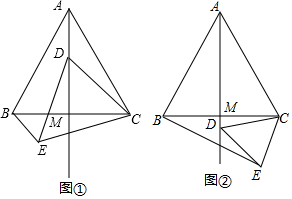
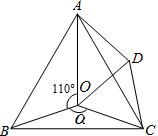 如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.
如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com