

分析 (1)结论:菱形.首先证明四边形ACEC′是平行四边形,再由AC=AC′即可证明结论.
(2)如图3中,过点A作AE⊥C′C于点E,首先证明DC′∥CB,DC′=BC,推出四边形BCC′D是平行四边形,再证明∠BCC′=900即可.
解答 解:(1)结论:菱形.
理由:如图2中,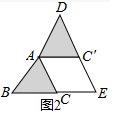
由题意∵AB=BC,
∴∠BAC=∠BCA=∠CAC′=∠AC′D
∴AC′∥EC,
∵∠CAC′=∠AC′D,
∴AC∥EC′,
∴四边形ACEC′是平行四边形,
∵AC=AC′,
∴四边形ACEC′是菱形.
(2)如图3中,过点A作AE⊥C′C于点E,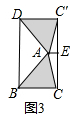
由旋转的性质,得AC′=AC,
∴∠CAE=∠C′AE=$\frac{1}{2}$α=∠ABC,∠AEC=90°,
∵BA=BC,
∴∠BCA=∠BAC
∴∠CAE=∠BCA,
∴AE∥BC.
同理,AE∥DC′,
∴BC∥DC′,
又∵BC=DC′,
∴四边形BCC′D是平行四边形,
又∵AE∥BC,∠AEC=90°,
∴∠BCC′=1800-900=900
∴四边形BCC′D是矩形.
点评 本题考查四边形综合题.矩形的判定和性质、菱形的判定和性质、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
如图,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
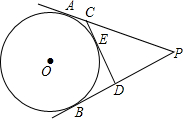 如图,PA、PB切⊙O于点A、B,CD是⊙O的切线,交PA、PB于C、D两点,△PCD的周长是36,则AP的长为( )
如图,PA、PB切⊙O于点A、B,CD是⊙O的切线,交PA、PB于C、D两点,△PCD的周长是36,则AP的长为( )| A. | 12 | B. | 18 | C. | 24 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y1<y2<y3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com