练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （本小题满分6分，请在下列两个小题中，任选其一完成即可）
    （1）解方程：x2+3x-2=0；
    （2）如图，在边长为1个单位长度的正方形方格纸中建立直角坐标系，△ABC各顶点的坐标为：A（-5，4）、B（-1，1）、C（-5，1）．
    ①将△ABC绕着原点O顺时针旋转90°得到△A′B′C′，请在图中画出△A′B′C′；
    ②写出A′点的坐标．
    分析：（1）利用求根公式法解方程；
    （2）①分别把点A、B、C绕着原点O顺时针旋转90°得到点A′、B′、C′，然后连结组成三角形；
    ②观察图形即可得到A′点的坐标．
    解答：解：（1）△=32-4×1×（-2）=17，
    x=
    -3±
    		17
    2
    ，
    所以x1=
    -3+
    		17
    2
    ，x2=
    -3-
    		17
    2
    ；
    （2）①如图，
    ②A′点的坐标为（4，5）．
    点评：本题考查了坐标与图形变化-旋转：图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．常见的是旋转特殊角度如：30°，45°，60°，90°，180°．也考查了解一元二次方程．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    加试题（本小题满分20分，其中（1）、（2）、（3）题各3分，（4）题11分）
    （1）一个正数的平方根为3-a和2a+3，则这个正数是
    81
    81

    （2）若x2+2x+y2-6y+10=0，则xy=
    -1
    -1

    （3）已知a，b分别是6-
    		13
    的整数部分和小数部分，则2a-b=
    		13
    		13

    （4）阅读下面的问题，并解答问题：
    1）如图1，等边△ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数是多少？（请在下列横线上填上合适的答案）
    分析：由于PA，PB，PC不在同一个三角形中，为了解决本题我们可以将△ABP绕顶点A逆时针旋转到△ACP′处，此时可以利用旋转的特征等知识得到：
      ①∠APB=∠AP′C=∠AP′P+∠PP′C；
      ②AP=AP′，且∠PAP′=
    60
    60
    度，所以△APP′为
    等边
    等边
    三角形，则∠AP′P=
    60
    60
    度；
      ③P′C=BP=4，P′P=AP=3，PC=5，所以△PP′C为
    直角
    直角
    三角形，则∠PP′C=
    90
    90
    度，从而得到∠APB=
    150
    150
    度．
     2）请你利用第1）题的解答方法，完成下面问题：
    如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为边BC上的点，且∠EAF=45°，试说明：EF2=BE2+FC2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （本题满分6分）小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明
    想建一个圆形花坛，使三棵树都在花坛的边上．
    （1）（本小题满分4分）请你帮小明把花坛的位置画出来（尺规作图，不写作法，保
    留作图痕迹）．
    （2）（本小题满分2分））若△ABC中AB=8米，AC=6米，∠BAC=，试求小明家圆形花坛的面积．

    查看答案和解析>>

    科目：初中数学 来源：2010年黄冈市语、数、英三科联赛九年级数学模拟试题C卷 题型：解答题

    （本小题满分10分）

    （1）如果△ABC的面积是S，E是BC的中点，连接AE（如图1），则△AEC的面积是            ；

    （2）在△ABC的外部作△ACD，F是AD的中点，连接CF（如图2），若四边形ABCD的面积是S，则四边形AECF的面积是             ；

    （3）若任意四边形ABCD的面积是S，E、F分别是一组对边AB、CD的中点，连接AF，CE（如图3），则四边形AECF的面积是             ；

    图1              图2                 图3

    拓展与应用

    （1）若八边形ABCDEFGH的面积是100，K、M、N、O、P、Q分别是AB、BC、CD、EF、FG、GH的中点，连接KH、MG、NF、OD、PC、QB、（如图4），则图中阴影部分的面积是             ；

    （2）四边形ABCD的面积是100，E、F分别是一组对边AB、CD上的点，且AE=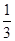AB，

     

    CF=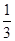CD，连接AF，CE（如图5），则四边形AECF的面积是             ；

     

    （3）（如图6）ABCD的面积是2，AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动，点F从点B出发沿BC以每秒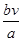个单位长的速度向点C运动.E、F分别从点A、B同时出发，当其中一点到达端点时，另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化？若不变，请写出这个值          ，并写出理由；若变化，说明是怎样变化的.

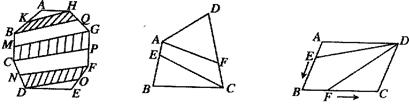
       图4                   图5                      图6

     

    查看答案和解析>>

    科目：初中数学 来源：2010年高级中等学校招生全国统一考试数学卷（江苏扬州） 题型：解答题

    （本小题满分14分）

    已知：如图，抛物线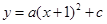与y轴交于点C（0，），  与x轴交于点A、 B，点A的坐标为（2，0）．

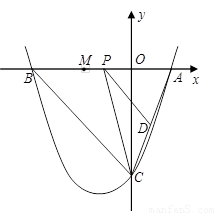
    （1）求该抛物线的解析式；

    （2）点P是线段AB上的动点，过点P作PD∥BC，交AC于点D，连接CP．当△CPD的面积最大时，求点P的坐标；

    （3）若平行于x轴的动直线与该抛物线交于点Q，与直线BC交于点F，点M 的坐标为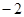（，0）．问：是否存在这样的直线，使得△OMF是等腰三角形？若存   在，请求出点Q的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    同步练习册答案