
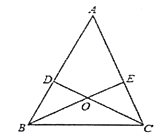
【题目】如图,已知AB=AC,AD=AE,BE与CD相交于O.图中全等的三角形有( )对.
A. 1 B. 2 C. 3 D. 4
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:初中数学 来源: 题型:
【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点到原点的距离相等.
(1)用“>”“=”“<”填空:b 0,a+b 0,a﹣c 0,b﹣c 0,a+c 0;
(2)化简|a+b|+|a﹣c|﹣|b|+|a|+|c|+|a+c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了拉动内需,全国各地汽车购置税补贴活动在2009年正式开始,某经销商在政策出台前一个月共售出某品牌汽车的手动型和自动型共960台,政策出台后的第一个月售出这两种型号的汽车共1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.
(1)在政策出台前一个月,销售的手动型和自动型汽车分别为多少台?
(2)若手动型汽车每台价格为8万元,自动型汽车每台价格为9万元.根据汽车补贴政策,政府按每台汽车价格的5%给购买汽车的用户补贴,问政策出台后的第一个月,政府对这1228台汽车用户共补贴了多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校校园内有一小山坡AB,经测量,坡角∠ABC=30°,斜坡AB长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD的坡比是1:3(即为CD与BC的长度之比).A,D两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)(3+![]() )(3﹣
)(3﹣![]() )﹣(1﹣
)﹣(1﹣![]() )2
)2
(3)我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选一个,并选择你认为适当的方法解这个方程.
①x2﹣4x﹣1=0 ②x(2x+1)=8x﹣3 ③x2+3x+1=0 ④x2﹣9=4(x﹣3)
我选择第几个方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药后,大约 分钟后,药物发挥作用.
(2)服药后,大约 小时,每毫升血液中含药量最大,最大值是 微克;
(3)服药后,药物发挥作用的时间大约有 小时.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE. 
(1)求证:AF=DE;
(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com