直线y=x-2分别交x轴、y轴于A、B两点,原点为O
(1)求△AOB的面积;
(2)求O到直线y=x-2的距离;
(3)是否存在过△AOB的顶点的直线L,把△AOB分成面积相等的两部分,若存在,写出直线L的解析式.
解:(1)如下图所示

∵直线y=x-2分别交x轴、y轴于A、B两点,
∴A、B点的坐标分别为(2,0)、(0,-2),
S
△AOB=
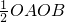
=
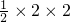
=2;
(2)从图中不难发现O到直线y=x-2的距离即为△AOB边AB边上的高,
∵AB=

=

,
∴△AOB边AB边上的高OE=

=

=

;

(3)①当过△AOB顶点O时,如图所示,E为直线L与直线AB的交点,
由题意及图知E为线段AB的中点,
∴E点的坐标为(1,-1),
则直线L的解析式为y=-x,
②当过△AOB顶点A时,如图所示,E为直线L与y轴的交点,

由题意及图知E为线段OB的中点,
∴E点的坐标为(0,-1),
则直线L的解析式为y-(-1)=

x,即

,
③当过△AOB顶点B时,如图所示,E为直线L与x轴的交点,

由题意及图知E为线段OA的中点,
∴E点的坐标为(-1,0),
则直线L的解析式为y+2=2x,即y=2x-2.
分析:(1)首先根据直线y=x-2分别交x轴、y轴于A、B两点,确定出A、B两点的坐标值.再运用S
△AOB=
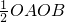
代入求得结果.
(2)由(1)不难确定△AOB是等腰直角三角形且O到直线y=x-2的距离即为△AOB边AB边上的高.运用三角形面积公式求得OE的长即可.
(3)因为△AOB有三个顶点,因而分三种情况:①当直线L过△AOB顶点O时;②当直线L过△AOB顶点A时;③当直线L过△AOB顶点B时讨论.对每种情况都要求得顶点对应边得中点坐标,再根据两点坐标确定直线L的解析式.
点评:本题是一次函数与三角形相结合的问题,在本题中多次用到利用两点坐标确定一次函数的解析式.


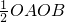 =
=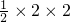 =2;
=2; =
= ,
, =
= =
= ;
;

 x,即
x,即 ,
,
 代入求得结果.
代入求得结果.

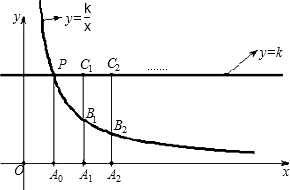 别作x轴的垂线,与双曲线y=
别作x轴的垂线,与双曲线y= A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.
A,直线y=-2x+1与抛物线交于点B,且与y轴、直线x=-2分别交于点D、C.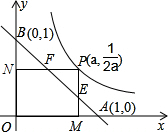 如图,P是函数y=
如图,P是函数y=