
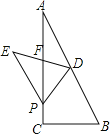
【题目】在Rt△ABC中,BC=4,AC=8,点D为AB的中点,P为AC边上一动点.△BDP沿着PD所在的直线翻折,点B的对应点为E.
(1)若PD⊥AB,求AP;
(2)若△PDE与△ABC重合部分的面积等于△PAB面积的![]() ,求AP的长.
,求AP的长.
【答案】(1)AP=5;(2)AP=6或2![]() .
.
【解析】
试题分析:(1)如图1,根据勾股定理可求出AB,从而得到AD、BD的值,易证△ADP∽△ACB,只需运用相似三角形的性质就可求出AP的值;
(2)根据条件可得S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
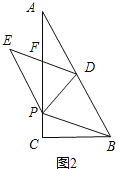
S△ADP=![]() S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2
S△EDP,从而可得AF=PF,EF=DF.而符合条件的位置有两个(图3、图4),需分两种情况讨论:①如图3,根据三角形中位线定理可得DF∥BP,则有∠EDP=∠BPD.由折叠可得∠BDP=∠EDP,从而可得∠BDP=∠BPD,即可得到BP=BD=2![]() ,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2
,在Rt△BCP中运用勾股定理可求出PC,就可得到AP的值;②如图4,连接AE,由AF=PF,EF=DF可得四边形AEDP是平行四边形,则有AP=ED,由折叠可得DE=DB,即可得到AP=DB=2![]() .
.
解:(1)如图:∵∠C=90°,BC=4,AC=8,
∴AB=4![]()
∵点D为AB的中点,
∴AD=DB=2![]()
∵PD⊥AB,
∴∠ADP=90°,
∵∠A=∠A,∠ADP=∠C,
∴△ADP∽△ACB,
∴![]() ,
,
∴AP=5;
(2)∵点D是线段AB的中点,
∴S△ADP=S△BDP=S△PAB.
由折叠可得:S△EDP=S△BDP,
∴S△PDF=![]() S△PAB=
S△PAB=![]() S△ADP=
S△ADP=![]() S△EDP,
S△EDP,
∴AF=PF,EF=DF.
①如图3,
根据三角形中位线定理可得:DF∥BP,
∴∠EDP=∠BPD.
由折叠可得∠BDP=∠EDP,
∴∠BDP=∠BPD,
∴BP=BD=2![]() ,
,
∴PC=![]() ,
,
∴AP=8﹣2=6;
②如图4,
连接AE,
∵AF=PF,EF=DF,
∴四边形AEDP是平行四边形,
∴AP=ED,
由折叠可得:DE=DB,
∴AP=DB=2![]() .
.
综上所述:AP=6或2![]() .
.





 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
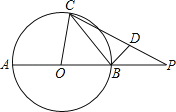
【题目】如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=2β.求证:tanαtanβ=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均成绩都相同,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,则射箭成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 周长相等的锐角三角形都全等
B. 周长相等的直角三角形都全等
C. 周长相等的钝角三角形都全等
D. 周长相等的等边三角形都全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列命题改写成为“如果……,那么……”的形式
(1)平行于同一条直线的两条直线平行;
(2)同角的余角相等;
(3)绝对值相等的两个数一定相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中,不能够判定一个四边形是平行四边形的是( )
A. 一组对边平行,另一组对边相等 B. 一组对边平行且相等
C. 两组对边分别平行 D. 对角线互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个木工师傅测量了一个等腰三角形木板的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮助他找出来,是第( )组.
A. 13,12,12 B. 12,12,8 C. 13,10,12 D. 5,8,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com