
 8
8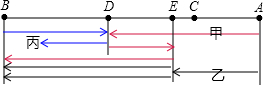
 t,
t, t,
t, vt=
vt= BD.
BD. t,
t, 、8.
、8.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建省泉州市泉港博文中学七年级3月月考数学试卷(带解析) 题型:解答题
甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务,若由这三人中的某一人独立完成阅卷任务,则甲需要15小时,乙需要10小时,丙需要8小时。
(1)如果甲、乙、丙三人同时改卷,那么需要多少时间完成?
(2)如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷,每一轮中每人各阅卷1小时。那么要多少小时完成?
(3)能否把(2)题所说的甲、乙、丙的次序作适当调整,其余的不变,使得完成这项任务的时间至少提前半小时?(答题要求:如认为不能,需要说明理由;如认为能,请至少说出一种轮流的次序,并求出相应能提前多少时间完成阅卷任务)
查看答案和解析>>
科目:初中数学 来源:2015届福建省泉州市七年级3月月考数学试卷(解析版) 题型:解答题
甲、乙、丙三个教师承担本学期期末考试的第17题的网上阅卷任务,若由这三人中的某一人独立完成阅卷任务,则甲需要15小时,乙需要10小时,丙需要8小时。
(1)如果甲、乙、丙三人同时改卷,那么需要多少时间完成?
(2)如果按照甲、乙、丙、甲、乙、丙、……的次序轮流阅卷,每一轮中每人各阅卷1小时。那么要多少小时完成?
(3)能否把(2)题所说的甲、乙、丙的次序作适当调整,其余的不变,使得完成这项任务的时间至少提前半小时?(答题要求:如认为不能,需要说明理由;如认为能,请至少说出一种轮流的次序,并求出相应能提前多少时间完成阅卷任务)
查看答案和解析>>
科目:初中数学 来源:期中题 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:
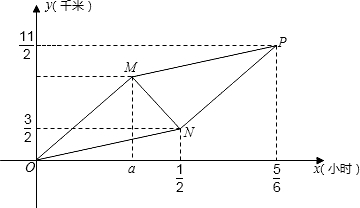
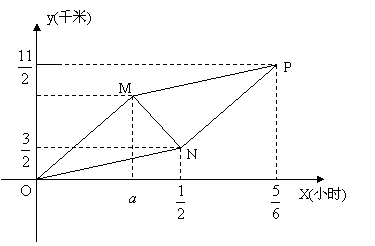
甲、乙、丙三人同时从A村出发去B村,刚开始甲骑自行车载乙,丙步行;![]() 小时后甲骑车中途回头接丙,乙步行,结果三人同时到达B地。假设:乙、丙步行速度相同,甲载乙与甲载丙时速度相同,甲载人与不载人时的速度不同,甲、乙、丙三人与A村之间的距离y(千米)与出发的时间x(小时)之间的函数关系如图。(掉头与上下车时间忽略不计)
小时后甲骑车中途回头接丙,乙步行,结果三人同时到达B地。假设:乙、丙步行速度相同,甲载乙与甲载丙时速度相同,甲载人与不载人时的速度不同,甲、乙、丙三人与A村之间的距离y(千米)与出发的时间x(小时)之间的函数关系如图。(掉头与上下车时间忽略不计)
(1)选择:甲与A村之间的距离y (千米)与出发时间x (小时)之间的函数图像为折线( ),
A.O-M-P B.O-N-P C.O-M-N-P D.O-N-M-P
乙与A村之间的距离y (千米)与出发时间x (小时)之间的函数图像为折线( ),
A.O-M-P B.O-N-P C.O-M-N-P D.O-N-M-P
丙与A村之间的距离y (千米)与出发时间x (小时)之间的函数图像为折线( )。
A.O-M-P B.O-N-P C.O-M-N-P D.O-N-M-P
(2)求步行速度,和甲载人骑车时的速度。
(3)求a的值以及甲骑车走过的总路程。(写出必要的演算和推理过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com