
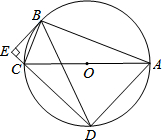
 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,AC=13,BC=5,弦BD=BA,BE⊥DC交DC的延长线于点E.| AC2-BC2 |
| BD |
| AC |
| DE |
| AB |
| 12 |
| 13 |
| DE |
| 12 |
| 144 |
| 13 |


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
 如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度d与时间t的函数关系的图象可能是( )
如图,⊙O上有两点A与P,且OA⊥OP,若A点固定不动,P点在圆上匀速运动一周,那么弦AP的长度d与时间t的函数关系的图象可能是( )
| A、① | B、③ | C、①或③ | D、②或④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、9 | B、-13 | C、-27 | D、7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 人 | 测试成绩 | ||
| 题目 | 甲 | 乙 | 丙 |
| 文化课知识 | 74 | 87 | 69 |
| 面试 | 58 | 74 | 70 |
| 平时表现 | 87 | 43 | 65 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x | … | -3 | 0 | 1 | … |
| y | … | 1 | 1 | 5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,甲、乙两人做转盘游戏,甲说:“我要顺时针转动转盘,当转盘停止时指针指向几就顺时针走几格,如果得偶数的1分,否则不得分!”乙说:“我要逆时针转动转盘,当转盘停止时指针指向几就逆时针走几格,如果得偶数的1分,否则不得分!”上面游戏公平吗?请说明理由.
如图,甲、乙两人做转盘游戏,甲说:“我要顺时针转动转盘,当转盘停止时指针指向几就顺时针走几格,如果得偶数的1分,否则不得分!”乙说:“我要逆时针转动转盘,当转盘停止时指针指向几就逆时针走几格,如果得偶数的1分,否则不得分!”上面游戏公平吗?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com