
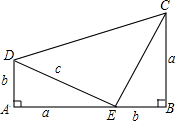
 如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗? 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
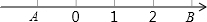 如图,在数轴上有A,B两点,A,B两点表示的有理数分别是a和b,a的倒数等于它本身,|b|=3,a<b且ab<0.
如图,在数轴上有A,B两点,A,B两点表示的有理数分别是a和b,a的倒数等于它本身,|b|=3,a<b且ab<0.| 7 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.
如图,在Rt△ABC中∠ABC=90°,以AB为直径作圆O交AC于E,连接E点和CB的中点D.查看答案和解析>>
科目:初中数学 来源: 题型:
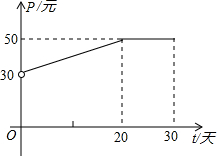 根据市场调查,某种新产品投放市场30天内,每件产品的销售价格
根据市场调查,某种新产品投放市场30天内,每件产品的销售价格| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com