
ЗжЮі ЃЈ1ЃЉШчЭМ1жаЃЌзїDHЁЭABгкHЃЌЪзЯШЧѓГіЕуAзјБъЃЌгЩOCЁЮDHЃЌЕУ$\frac{AC}{CD}$=$\frac{OA}{OH}$=$\frac{1}{4}$ЃЌгЩOA=1ЃЌЭЦГіOH=4ЃЌЭЦГіDЃЈ4ЃЌ-$\frac{5}{2}$ЃЉЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпlЕФНтЮіЪНМДПЩЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌСЌНгEAЁЂECЃЌзїEKЁЮOCНЛADгкKЃЌЩшEЃЈmЃЌ-$\frac{1}{2}$m2+m+$\frac{3}{2}$ЃЉЃЌдђKЃЈmЃЌ-$\frac{1}{2}$m-$\frac{1}{2}$ЃЉЃЌEK=-$\frac{1}{2}$m2+$\frac{3}{2}$m+2ЃЎИљОнSЁїACE=SЁїAEK-SЁїCEKЃЌЙЙНЈЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉДцдкЃЎШчЭМ3жаЃЌЕБADЮЊОиаЮЕФЖдНЧЯпЪБЃЌЩшЖдНЧЯпЕФНЛЕуЮЊNЃЎPЃЈ1ЃЌbЃЉЃЎИљОнЬтвтPN=AN=DN=$\frac{5\sqrt{5}}{4}$ЃЌПЩЕУЗНГЬЃЈ$\frac{5\sqrt{5}}{4}$ЃЉ2=ЃЈ1-$\frac{3}{2}$ЃЉ2+ЃЈb+$\frac{5}{4}$ЃЉ2ЃЌЧѓГіЕуPзјБъЃЌдйРћгУжаЕузјБъЙЋЪНЃЌЧѓГіЕуQзјБъЃЌМьбщЕуQЪЧЗёдкХзЮяЯпЩЯЃЌМДПЩНтОіЮЪЬтЃЎ
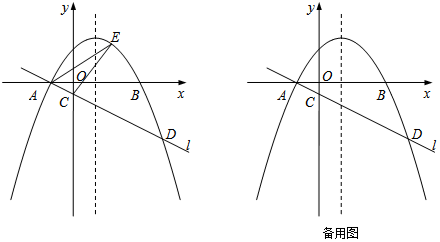
НтД№ НтЃКЃЈ1ЃЉШчЭМ1жаЃЌзїDHЁЭABгкHЃЎ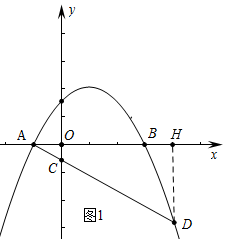
ЖдгкХзЮяЯпy=-$\frac{1}{2}$x2+x+$\frac{3}{2}$ЃЌСюy=0ЃЌЕУ-$\frac{1}{2}$x2+x+$\frac{3}{2}$=0ЃЌНтЕУx=-1Лђ3ЃЌ
ЁрAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌ
ЁпOCЁЮDHЃЌ
Ёр$\frac{AC}{CD}$=$\frac{OA}{OH}$=$\frac{1}{4}$ЃЌЁпOA=1ЃЌ
ЁрOH=4ЃЌ
ЁрDЃЈ4ЃЌ-$\frac{5}{2}$ЃЉЃЌ
ЩшжБЯпADЕФНтЮіЪНЮЊy=kx+bдђга$\left\{\begin{array}{l}{-k+b=0}\\{4k+b=-\frac{5}{2}}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$ЃЌ
ЁржБЯпlЕФНтЮіЪНЮЊy=-$\frac{1}{2}$x-$\frac{1}{2}$ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌСЌНгEAЁЂECЃЌзїEKЁЮOCНЛADгкKЃЌЩшEЃЈmЃЌ-$\frac{1}{2}$m2+m+$\frac{3}{2}$ЃЉЃЌдђKЃЈmЃЌ-$\frac{1}{2}$m-$\frac{1}{2}$ЃЉЃЌEK=-$\frac{1}{2}$m2+$\frac{3}{2}$m+2ЃЎ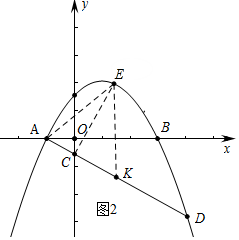
ЁпSЁїACE=SЁїAEK-SЁїCEK=$\frac{1}{2}$ЁСЃЈ-$\frac{1}{2}$m2+$\frac{3}{2}$m+2ЃЉЁСЃЈm+1ЃЉ-$\frac{1}{2}$ЁСЃЈ-$\frac{1}{2}$m2+$\frac{3}{2}$m+2ЃЉЁСm=-$\frac{1}{4}$m2+$\frac{3}{4}$m+1=-$\frac{1}{4}$ЃЈm-$\frac{3}{2}$ЃЉ2+$\frac{25}{16}$ЃЌ
Ёп-$\frac{1}{4}$ЃМ0ЃЌ
Ёрm=$\frac{3}{2}$ЪБЃЌЁїACEЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ$\frac{25}{16}$ЃЎ
ЃЈ3ЃЉДцдкЃЎШчЭМ3жаЃЌЕБADЮЊОиаЮЕФЖдНЧЯпЪБЃЌЩшЖдНЧЯпЕФНЛЕуЮЊNЃЎPЃЈ1ЃЌbЃЉЃЎ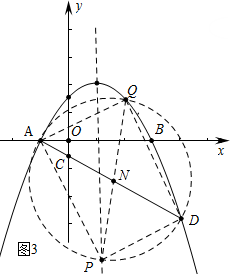
ЁпAЃЈ-1ЃЌ0ЃЉЃЌDЃЈ4ЃЌ-$\frac{5}{2}$ЃЉЃЌ
ЁрNЃЈ$\frac{3}{2}$ЃЌ-$\frac{5}{4}$ЃЉЃЌAD=$\sqrt{{5}^{2}+ЃЈ\frac{5}{2}ЃЉ^{2}}$=$\frac{5\sqrt{5}}{2}$ЃЌ
ЁпЁЯAPD=90ЁуЃЌ
ЁрPN=AN=DN=$\frac{5\sqrt{5}}{4}$ЃЌ
ЁрЃЈ$\frac{5\sqrt{5}}{4}$ЃЉ2=ЃЈ1-$\frac{3}{2}$ЃЉ2+ЃЈb+$\frac{5}{4}$ЃЉ2ЃЌ
НтЕУb=-4Лђ$\frac{3}{2}$ЃЈВЛКЯЬтвтЩсЦњЃЉЃЌ
ЁрPЃЈ1ЃЌ-4ЃЉЃЌ
ЁпPN=NQЃЌAN=NDЃЌ
ЁрQЃЈ2ЃЌ$\frac{3}{2}$ЃЉЃЌ
ЖдгкХзЮяЯпy=-$\frac{1}{2}$x2+x+$\frac{3}{2}$ЃЌ
Ёпx=2ЪБЃЌy=$\frac{3}{2}$ЃЌ
ЁрЕуQЃЈ2ЃЌ$\frac{3}{2}$ЃЉдкХзЮяЯпЩЯЃЌ
ЁрвдЕуAЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮФмГЩЮЊОиаЮЃЌДЫЪБЕуPзјБъЃЈ1ЃЌ-4ЃЉЃЎ
ЕуЦР БОЬтПМВщЖўДЮКЏЪ§злКЯЬтЁЂвЛДЮКЏЪ§ЕФгІгУЁЂОиаЮЕФХаЖЈКЭаджЪЃЌжаЕузјБъЙЋЪНЁЂЙДЙЩЖЈРэЕШжЊЪЖЃЌНтЬтЕФЙиМќЪЧбЇЛсЙЙНЈЖўДЮКЏЪ§НтОізюжЕЮЪЬтЃЌбЇЛсгУЗНГЬЕФЫМЯыЫМПМЮЪЬтЃЌЪєгкжаПМбЙжсЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌвбжЊЁбOЕФжБОЖABгыЯвCDЛЅЯрДЙжБЃЌДЙзуЮЊEЃЌЁбOЕФЧаЯпBFгыЯвADЕФбгГЄЯпЯрНЛгкЕуFЃЌЧвOA=3ЃЌBE=2ЃЎ
ШчЭМЃЌвбжЊЁбOЕФжБОЖABгыЯвCDЛЅЯрДЙжБЃЌДЙзуЮЊEЃЌЁбOЕФЧаЯпBFгыЯвADЕФбгГЄЯпЯрНЛгкЕуFЃЌЧвOA=3ЃЌBE=2ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
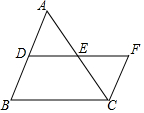 ШчЭМЃЌDEЪЧЁїABCЕФжаЮЛЯпЃЌбгГЄDEжСFЪЙEF=DEЃЌСЌНгCFЃЌдђSЁїADEЃКSЫФБпаЮBCFDЕФжЕЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЌDEЪЧЁїABCЕФжаЮЛЯпЃЌбгГЄDEжСFЪЙEF=DEЃЌСЌНгCFЃЌдђSЁїADEЃКSЫФБпаЮBCFDЕФжЕЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 1ЃК3 | BЃЎ | 2ЃК3 | CЃЎ | 2ЃК5 | DЃЎ | 1ЃК4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
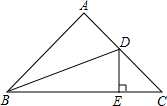 дк45ЁуЕФRtЁїABCжаЃЌЁЯA=90ЁуЃЌDEЁЭBCЃЌBDЪЧЁЯABCЕФЦНЗжЯпЃЌЧвBD=13ЃЌAB=12ЃЌдђЁїDECЕФжмГЄЮЊЃЈЁЁЁЁЃЉ
дк45ЁуЕФRtЁїABCжаЃЌЁЯA=90ЁуЃЌDEЁЭBCЃЌBDЪЧЁЯABCЕФЦНЗжЯпЃЌЧвBD=13ЃЌAB=12ЃЌдђЁїDECЕФжмГЄЮЊЃЈЁЁЁЁЃЉ| AЃЎ | 10$\sqrt{2}$ | BЃЎ | 5+$\sqrt{2}$ | CЃЎ | 10+$\sqrt{2}$ | DЃЎ | 17 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com