

 ,∠PBA =
,∠PBA = ,
, ,
, (cm)
(cm)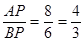 。
。

 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 和
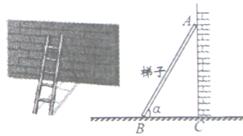
和 (均与水平面垂直),再将集热板安装在
(均与水平面垂直),再将集热板安装在 上.为使集热板吸热率更高,公司规定:
上.为使集热板吸热率更高,公司规定: 与水平面夹角为
与水平面夹角为 ,且在水平线上的射影
,且在水平线上的射影 为
为 .现已测量出屋顶斜面与水平面夹角为
.现已测量出屋顶斜面与水平面夹角为 ,并已知
,并已知 ,
, 。如果安装工人确定支架
。如果安装工人确定支架 高为
高为 ,求支架
,求支架 的高(结果精确到
的高(结果精确到 )?
)?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.(结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com